Giải bài 72 tr 51 sách BT Toán lớp 7 Tập 2
Cho \(H\) là trực tâm của tam giác \(ABC\) không vuông. Tìm trực tâm của các tam giác \(HAB, HAC, HBC.\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
Sử dụng: Ba đường cao của tam giác cùng đi qua một điểm. Điểm đó gọi là trực tâm của tam giác.
Lời giải chi tiết
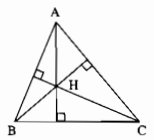
Trong ∆ABC ta có H là trực tâm nên
\(AH \bot BC,BH \bot AC,CH \bot AB\)
Trong ∆AHB ta có:
\(\eqalign{
& AC \bot BH \cr
& BC \bot AH \cr} \)
Hai đường cao kẻ từ A và B cắt nhau tại C.
Vậy C là trực tâm của ∆AHB.
Trong ∆HAC ta có:
\(\eqalign{
& BA \bot CH \cr
& CB \bot BH \cr} \)
Hai đường cao kẻ từ A và C cắt nhau tại B, Vậy B là trực tâm của ∆HAC.
Trong ∆HBC ta có:
\(\eqalign{
& BA \bot HC \cr
& CA \bot BH \cr} \)
Hai đường cao kẻ từ B và C cắt nhau tại A. Vậy A là trực tâm của ∆HBC.
-- Mod Toán 7 HỌC247
-


Cho góc nhọn xOy và K là một điểm thuộc tia phân giác của góc xOy. Kẻ KA vuông góc với Ox (A thuộc Ox), KB vuông góc với Oy ( B thuộc Oy). Chứng minh: KA = KB.
bởi Học Hành
 20/02/2020
20/02/2020
Cho góc nhọn xOy và K là một điểm thuộc tia phân giác của góc xOy. Kẻ KA vuông góc với Ox (A thuộc Ox), KB vuông góc với Oy ( B thuộc Oy) a. Chứng minh: KA = KB. b. Tam giác OAB là tam giác gì? Vì sao? c. Đường thẳng BK cắt Ox tại D, đường thẳng AK cắt Oy tại E. Chứng minh: KD = KE. d. Chứng minh OK vuông góc DE
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC có A= 90 độ. Trên cạnh BC lấy điểm E sao cho BE=BA. Tia phân giác của góc B cắt Ac ở D. Chứng minh tam giác ABD = tam giác EBD
bởi Milk Pé
 20/02/2020
20/02/2020
Cho tam giác ABC có A= 90 độ. Trên cạnh BC lấy điểm E sao cho BE=BA. Tia phân giác của góc B cắt Ac ở D.
a, Chứng minh tam giác ABD = tam giác EBD
b, Chứng minh BC vuông góc với DE
c, Trên tia đối của tia ED lấy điểm F sao cho È= ED. CHứng minh BFE= DBC+DCB
Theo dõi (0) 0 Trả lời -


Tính tổng S=1x4+2x5+3x6+4x7+...+n(n+3)
bởi black hope
 20/02/2020
20/02/2020
tính tổng : S=1x4+2x5+3x6+4x7+...+n(n+3) với n=1,2,3,..
Theo dõi (0) 0 Trả lời -


Cho tam giác ABC có A= 90 độ. Trên cạnh BC lấy điểm E sao cho BE=BA. Tia phân giác của góc B cắt AC ở D. Chứng minh tam giác ABD= tam giác EBD
bởi Milk Pé
 20/02/2020
20/02/2020
Bài 1:Cho tam giác ABC có A= 90 độ. Trên cạnh BC lấy điểm E sao cho BE=BA. Tia phân giác của góc B cắt AC ở D.
a, Chứng minh tam giác ABD= tam giác EBD
b, Chứng minh: BC vuông góc với DE
c, Trên tia đối của tia ED lấy điểm F sao cho È= ED. CHứng minh BFE= DBC+DCB
Theo dõi (0) 0 Trả lời -


Chứng minh rằng a và b đều chia hết cho 3 biết a, b nguyên thỏa mãn a^2 - ab + b^2 chia hết cho 9
bởi Vladislav Hoàng
 18/02/2020
18/02/2020
Cho a, b nguyên thỏa mãn
chia hết cho 9. Chứng minh rằng a và b đều chia hết cho 3.
Theo dõi (0) 4 Trả lời -


Cho tam giác ABC vuông tại A, tia phân giác BD. Kẻ DH vuông góc với BC (H € BC)
a) Chứng minh rằng .
b) Chứng minh rằng DA = DH.
c) Tam giác BAH là tam giác gì? Vì sao?
d) Trên tia đối của tia AB lấy điểm F sao cho AF = HC. Chứng minh rằng .
e) Tìm điều kiện của tam giác ABC để đều.Theo dõi (0) 5 Trả lời -


Tìm điều kiện của tam giác ABC để đều
bởi Tạ Hải Đăng
 18/02/2020
18/02/2020
Cho tam giác ABC vuông tại A, tia phân giác BD. Kẻ .
a) Chứng minh rằng .
b) Chứng minh rằng DA = DH.
c) Tam giác BAH là tam giác gì? Vì sao?
d) Trên tia đối của tia AB lấy điểm F sao cho AF = HC. Chứng minh rằng .
e) Tìm điều kiện của tam giác ABC để đều.Theo dõi (0) 1 Trả lời -


Tìm số đo góc lớn nhất trong tam giác ABC
bởi An Aeris
 18/02/2020
18/02/2020
Tam giác ABC có AB = 9cm, AC = 41cm và BC = 40cm. Số đo góc lớn nhất trong tam giác là
Theo dõi (1) 4 Trả lời -


Chứng minh ba điểm E, A, D thẳng hàng biết M, N là trung điểm của AC, AB
bởi phạm quốc Hưng
 12/02/2020
12/02/2020
Cho tam giác ABC. Gọi M, N lần lượt là trung điểm của các cạnh AC, AB. Trên Các đường thẳng BM và CN lần lượt lấy các điểm D và E sao cho M là trung điểm BD và N là trung điểm EC. Chứng minh ba điểm E, A, D thẳng hàng.
Theo dõi (0) 0 Trả lời -


Cho tam giác ABC vuông tại A (AB < AC), gọi O là trung điểm của BC, trên tia đối của tia OA lấy điểm K sao cho OA = OK. Vẽ AH vuông góc với BC tại H, trên tia HC lấy HD = HA. Đường vuông góc với BC tại D cắt AC tại E. Chứng minh AB = AE
bởi Khan H CHi
 12/02/2020
12/02/2020
Cho tam giác ABC vuông tại A (AB < AC), gọi O là trung điểm của BC, trên tia đối của tia OA lấy điểm K sao cho OA = OK. Vẽ AH vuông góc với BC tại H, trên tia HC lấy HD = HA. Đường vuông góc với BC tại D cắt AC tại E.
1. Chứng minh AB = AE
2. Gọi M là trung điểm của BE. Tính số đo góc CHM.
3. Chứng minh:1/AB^2 + 1/AC^2 = 1/AH^2Theo dõi (0) 0 Trả lời -


Cho tam giác ABC cân tại A và Â<90 độ kẻ BD vuông góc với AC. Trên cạnh AB lấy điểm E sao cho AE=AD. Chứng minh: DE//BC
bởi nguyễn duy tình
 12/02/2020
12/02/2020
a, cho tam giác ABC có góc A;B;C tỉ lệ với 7;5;3 . Các góc ngoài tương ứng tỉ lệ với sồ nào
b,cho tam giác ABC cân tại A và Â<90 độ kẻ BD vuông góc với AC .Trên cạnh AB lấy điểm E sao cho AE=AD .chứng minh :
1,DE song song BC
2,CE vuông góc AB
Theo dõi (0) 0 Trả lời -


Tìm số nguyên x và y biết 5/x+y/4=1/8
bởi nguyễn duy tình
 12/02/2020
12/02/2020
a, tìm số nguyên x và y biết : 5/x+y/4=1/8
b,tìm số nguyên x để A có giá trị là 1 số nguyên biết A= căn x+1/căn x-3 (x > hoặc = 0)
Theo dõi (0) 0 Trả lời -


Tìm x biết (x-1)^5=-243
bởi nguyễn duy tình
 12/02/2020
12/02/2020
tìm x
a,(x-1)^5=-243
b,x+2/11+x+2/12+x+2/13=x+2/14+x+2/15
c,x-2.căn x=0
Theo dõi (0) 0 Trả lời -


Tìm x biết 2|5x-3|-2x=14
bởi nguyễn duy tình
 12/02/2020
12/02/2020
tìm x biết 2|5x-3|-2x=14
Theo dõi (2) 9 Trả lời -


Tính đoạn thẳng AB, AC biết BC=13cm, BH=9cm và HC=4cm
bởi lee vannn
 10/02/2020
10/02/2020
Cho ba điểm B, H,C sao cho BC=13cm,BH=9cm và HC=4cm.Qua H kẻ đường thẳng Hx vuông góc với đường thẳng BC và trên tia Hx lấy điểm A sao cho AH=6cm.
a)Tính đoạn thẳng AB,AC
b)Chứng minh AB vuông góc AC
Theo dõi (0) 1 Trả lời -


Tính 8^5 .(−5)^8 +(−2)^5 .10^9
bởi Yugi Muto
 10/02/2020
10/02/2020
Tính 8^5 .(−5)^8 +(−2)^5 .10^9 / 2^16.5^7+20^8
Theo dõi (0) 2 Trả lời -


Tính 1/10+1/100+1/1000+...+1/1000000
bởi Bảo Châuu
 10/02/2020
10/02/2020
1/10+1/100+1/1000+...+1/1000000
Theo dõi (0) 2 Trả lời -


tìm giá trị nhỏ nhất của : A=|x-a|+|x-b|+|x-c|+|x-d| với a<b<c<d
Theo dõi (0) 5 Trả lời -


Chứng minh I là trung điểm của AN
bởi suzanna dezaki
 08/02/2020
08/02/2020
cho tam giac ABC co AC<BC tren BC lay cac điểm M N sao cho BM=MN=CN .
Qua điểm M kẻ đường thẳng song song với AB cắt AN tai I
a) CM I là trung điểm của AN
b) Qua K kẻ dường thẳng vuông góc với tia phân giác góc ACB cat AC tại E cắt BC taih F CM AE=BF
Theo dõi (0) 0 Trả lời -


Tam giác ABC cân tại A, M là trung điểm của BC. Chứng minh AM vuông góc BC
bởi Phạm Anh Kiệt
 07/02/2020
07/02/2020
tam giác ABC cân tại a M là trung điểm của BC
Câu a chứng minh AM vuông góc BC
Câu b ME vuông góc AB tại E ,MF vuông góc AC tại F chứng minh ME = MF
Câu c chứng minh EF song song BC
Câu d EMcắt AC tại K , FM cắt AB tại H tìm điều kiện chứng minh tam giác AHK đều
Theo dõi (0) 0 Trả lời -


Chứng minhnếu trừ các giá trị của dấu hiệu đi cùng một số thì số trung bình của dấu hiệu cũng được trừ đi số đó
bởi Vi Hồng
 07/02/2020
07/02/2020
Chứng tỏ rằng nếu trừ các giá trị của dấu hiệu đi cùng một số thì số trung bình của dấu hiệu cũng được trừ đi số đó
Theo dõi (0) 0 Trả lời -


Cho ∆ABC cân tại A. Lấy điểm M thuộc AB, N thuộc AC sao cho BM=CN. Gọi O là giao điểm của BN và CM. CMR: ∆AMN cân, từ đó suy ra MN//BC; ∆BMO=∆CNO.
bởi Vũ Phúc
 07/02/2020
07/02/2020
cho tam giác ABC cân tại A. Lấy điểm M thuộc AB, N thuộc AC sao cho BM=CN. Gọi O là giao điểm của BN và CM. CMR
A tam giác AMN cân , từ đó suy ra MN//BC
B tam giác BMO= tam giác CNO
Theo dõi (1) 0 Trả lời -


tìm x thuộc N để A=(căn bậc x)+2/(căn bậc x)-3 là số nguyên
Theo dõi (0) 0 Trả lời -


Cho ΔABC cân tại A. Kẻ BD⊥AC(D∈AC), CE⊥AB(E∈AB).
a) Chứng minh DE//BC
b) Gọi O là giao điểm của BD và CE. Chứng minh ΔEOB=ΔDOC
c) Chứng minh AO là trung trực của DE
d) Gọi H là trung điểm BC. Chứng minh A,O,H thẳng hàng
Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 70 trang 50 SBT Toán 7 Tập 2
Bài tập 71 trang 50 SBT Toán 7 Tập 2
Bài tập 73 trang 51 SBT Toán 7 Tập 2
Bài tập 74 trang 51 SBT Toán 7 Tập 2
Bài tập 75 trang 51 SBT Toán 7 Tập 2
Bài tập 76 trang 51 SBT Toán 7 Tập 2
Bài tập 77 trang 51 SBT Toán 7 Tập 2
Bài tập 78 trang 51 SBT Toán 7 Tập 2
Bài tập 79 trang 51 SBT Toán 7 Tập 2





