Bài tập 8 trang 126 SGK Hình học 11 NC

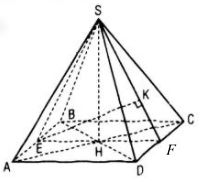
Gọi H là giao điểm của AC và BD. Do S.ABCD là hình chóp đều nên SH vuông góc với mặt đáy (ABCD).

a. Khoảng cách từ S đến mp(ABCD) là SH.

SAC là tam giác đều cạnh \(a\sqrt 2 \) 

Nên \(SH = a\sqrt 2 .\frac{{\sqrt 3 }}{2} = \frac{{a\sqrt 6 }}{2}\)

b. Gọi E, F lần lượt là trung điểm của AB và CD.

Ta có: d(AB ; (SCD)) = d(E; (SCD)) = EK

(EK là đường cao của tam giác SEF).

\(\begin{array}{l}
EK = \frac{{EF.SH}}{{SF}} = \frac{{a.\frac{{a\sqrt 6 }}{2}}}{{\sqrt {\frac{{6{a^2}}}{4} + \frac{{{a^2}}}{4}} }}\\
 = \frac{{a\sqrt 6 }}{{\sqrt 7 }} = \frac{{a\sqrt {42} }}{7}
\end{array}\)

c. Vì AB và SC chéo nhau, AB // mp(SCD) nên d(AB ; SC) = d(AB ; (SCD)) = \(\frac{{a\sqrt {42} }}{7}\)

d.

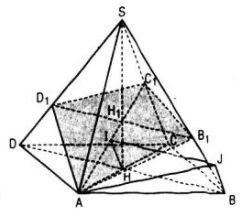
Gọi C₁ là trung điểm của SC, do SAC là tam giác đều nên AC₁ ⊥ SC. Mặt khác, BD ⊥ SC, nên (P) chính là mặt phẳng chứa AC₁ và song song với BD. Kí hiệu H₁ là giao điểm của AC₁ và SH. Khi đó (P) ∩ (SBD) = B₁D₁, trong đó B₁D₁ đi qua H₁ và song song với BD. Vậy thiết diện của S.ABCD cắt bởi (P) là tứ giác AB₁C₁D₁.

Ta có: BD ⊥ (SAC), B₁D₁ // BD

Nên B₁D₁ ⊥ (SAC), suy ra B₁D₁ ⊥ AC₁.

Từ đó \({S_{A{B_1}{C_1}{D_1}}} = \frac{1}{2}A{C_1}.{B_1}{D_1}\)

\(A{C_1} = \frac{{a\sqrt 6 }}{2},{B_1}{D_1} = \frac{2}{3}BD\) 

(vì H₁ là trọng tâm tam giác SAC)

Vì vậy \({S_{A{B_1}{C_1}{D_1}}} = \frac{1}{2}.\frac{{a\sqrt 6 }}{2}.\frac{2}{3}a\sqrt 2  = \frac{{{a^2}\sqrt 3 }}{3}\)

e. Trong mp(SAC), kẻ HI song song với CC₁ cắt AC1 tại I thì HI ⊥ (P) vì SC ⊥ (P).

Ta lấy điểm J sao cho BHIJ là hình bình hành thì BJ ⊥ (P), từ đó \(\widehat {BAJ}\) là góc giữa BA và mp(P).

\(\begin{array}{l}
\sin \widehat {BAJ} = \frac{{BJ}}{{BA}} = \frac{{HI}}{{BA}} = \frac{{\frac{1}{2}C{C_1}}}{{BA}}\\
 = \frac{{\frac{1}{4}SC}}{{BA}} = \frac{{\frac{1}{4}a\sqrt 2 }}{a} = \frac{{\sqrt 2 }}{4}
\end{array}\)

Vậy góc giữa BA và mp(P) là α

Mà \(\sin \alpha  = \frac{{\sqrt 2 }}{4},{0^ \circ } < \alpha  < {90^ \circ }.\)$$

-- Mod Toán 11 HỌC247