Giải bài 2 tr 199 SBT Hình học 11
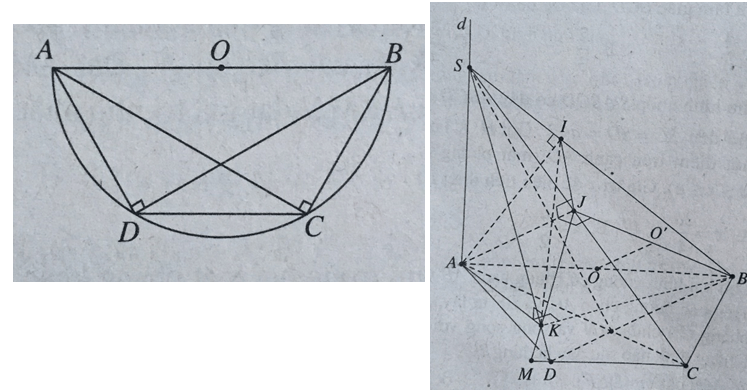
Cho hình thang ABCD có AB // CD và AB = 2a, BC = CD = DA = a. Đường thẳng d vuông góc với mặt phẳng (ABCD) tại A. Gọi S là một điểm duy nhất thay đổi trên d. (P) là một mặt phẳng qua A vuông góc với SB tại I và cắt SC, SD lần lượt tại J, K.
a) Chứng minh tứ giác BCJI, AIJK là các tứ giác nội tiếp.
b) Gọi O là trung điểm của AB, O' là tâm đường tròn ngoại tiếp tứ giác BCJI. Chứng minh rằng OO' ⊥ (SBC).
c) Chứng minh rằng khi S thay đổi trên d thì JK luôn luôn đi qua một điểm cố định.
d) Tìm một điểm cách đều các điểm A, B, C, D, I, J, K và tìm khoảng cách đó.
e) Gọi M là giao điểm của JK và (ABCD). Chứng minh rằng AM là tiếp tuyến của đường tròn ngoại tiếp tam giác ABC.
f) Khi S thay đổi trên d, các điểm I, J, K lần lượt chạy trên đường nào.
Hướng dẫn giải chi tiết
Nhận xét
Hình thang ABCD có hai cạnh bên và đáy nhỏ bằng nhau và bằng nửa đáy lớn, nên nó là nửa lục giác đều nội tiếp trong đường tròn đường kính AB, tâm O là trung điểm của AB.
Như vậy: \(\widehat {ACB} = \widehat {ADB} = 1v\).
a) Theo giả thiết, ta có: SA ⊥ (ABCD) ⇒ SA ⊥ BC
\(\left\{ \begin{array}{l}
BC \bot SA\\
BC \bot AC
\end{array} \right. \Rightarrow BC \bot \left( {SAC} \right) \Rightarrow BC \bot SC\,\,\left( 1 \right)\)
Mặt khác SB ⊥ (P) nên SB ⊥ IJ (⊂ (P)) (2)
Từ (1) và (2) suy ra BCJI là tứ giác nội tiếp trong đường tròn đường kính BJ.
Ta có BC ⊥ (SAC) ⇒ BC ⊥ AJ (⊂ (SAC))
\(\left\{ \begin{array}{l}
AJ \bot BC\\
AJ \bot SB
\end{array} \right. \Rightarrow AJ \bot \left( {SBC} \right) \Rightarrow AJ \bot JI\,\,\left( 3 \right)\)
Lý luận tương tự, ta có:
\(\left\{ \begin{array}{l}
BD \bot AD\\
BD \bot SA
\end{array} \right. \Rightarrow BD \bot \left( {SAD} \right) \Rightarrow BD \bot AK\)
\(\left\{ \begin{array}{l}
AK \bot BD\\
AK \bot SB
\end{array} \right. \Rightarrow AK \bot \left( {SBD} \right) \Rightarrow AK \bot KI\,\,\left( 4 \right)\)
Từ (3) và (4) suy ra AKJI nội tiếp trong đường tròn đường kính AI nằm trong mặt phẳng (P).
b) Ta có ngay O’ là trung điểm BJ
Vì OO’ là đường trung bình của ΔABJ nên OO’ // AJ
Mà AJ ⊥ (SBC) nên OO’ ⊥ (SBC)
c) Ta có (SCD) ∩ (ABCD) = CD.
Gọi M = JK ∩ CD
SA ⊥ (ABCD) ⇒ SA ⊥ AM(⊂ (ABCD)) (5)
SB ⊥ (P) ⇒ SB ⊥ AM (⊂ (P)) (6)
Từ (5) và (6), ta có: AM ⊥ (SAB) ⇒ AM ⊥ AB.
Suy ra AM là tiếp tuyến của đường tròn ngoại tiếp ΔABC tại A. Như vậy AM cố định. Vì M = AM ∩ CD nên M cố định.
d) ΔAIB vuông tại I nên OA = OB = OI
ΔAJB vuông tại J (do AJ ⊥ (SBC)) nên OA = OB = OJ).
ΔAKB vuông tại K (do AK ⊥ (SBD)) nên OA = OB = OK).
Ta có OA = OB = OC = OD = OI = OJ = OK nên O là điểm cách đều các điểm đã cho và OA = AB/2 = a.
e) Theo chứng minh câu c.
f) Khi S thay đổi trên d, ta có I luôn nằm trong mặt phẳng (B, d).
Trong mặt phẳng này I luôn nhìn đoạn AB cố định dưới góc vuông nên tập hợp I là đường tròn (C1) đường kính AB nằm trong mặt phẳng (B, d).
Tương tự, tập hợp J là đường tròn (C2) đường kính AC nằm trong mặt phẳng (C, d) và tập hợp K là đường tròn đường kính AD nằm trong mặt phẳng (D, d).
-- Mod Toán 11 HỌC247
-


Ở trong mặt phẳng tọa độ \(Oxy\), cho đường thẳng \(d\) có phương trình \(3x - y - 3 = 0\). Phép biến hình có được bằng cách thực hiện liên tiếp phép vị tự tâm \(I\left( {2;3} \right)\) tỉ số \(k = - 1\) và phép tịnh tiến theo vectơ \(\overrightarrow v \left( {1;3} \right)\) biến đường thẳng \(d\) thành đường thẳng \(d'\). Viết phương trình đường thẳng \(d'\).
bởi Spider man
 17/07/2021
17/07/2021
A. \(3x - y + 3 = 0\) B. \(3x + y + 3 = 0\) C. \(3x + y - 3 = 0\) D. \(3x - y - 3 = 0\)
Theo dõi (0) 1 Trả lời -


Ở trong mặt phẳng tọa độ \(Oxy,\) cho đường thẳng \(d:2x - y - 1 = 0.\) Hãy viết phương trình đường thẳng \(d'\) là ảnh của đường thẳng \(d\) qua phép tịnh tiến theo véc tơ \(\overrightarrow u = \left( {3; - 1} \right).\)
bởi Phí Phương
 17/07/2021
17/07/2021
Ở trong mặt phẳng tọa độ \(Oxy,\) cho đường thẳng \(d:2x - y - 1 = 0.\) Hãy viết phương trình đường thẳng \(d'\) là ảnh của đường thẳng \(d\) qua phép tịnh tiến theo véc tơ \(\overrightarrow u = \left( {3; - 1} \right).\)
Theo dõi (0) 1 Trả lời -


Với trong mặt phẳng tọa độ \(Oxy,\) cho hai điểm \(M\left( {4;6} \right)\) và \(M'\left( { - 3;5} \right).\) Phép vị tự tâm \(I\) tỉ số \(k = \dfrac{1}{2}\) biến điểm \(M\) thành điểm \(M'.\) Tìm tọa độ điểm \(I.\)
bởi Ánh tuyết
 17/07/2021
17/07/2021
Với trong mặt phẳng tọa độ \(Oxy,\) cho hai điểm \(M\left( {4;6} \right)\) và \(M'\left( { - 3;5} \right).\) Phép vị tự tâm \(I\) tỉ số \(k = \dfrac{1}{2}\) biến điểm \(M\) thành điểm \(M'.\) Tìm tọa độ điểm \(I.\)
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 5 trang 200 SBT Hình học 11
Bài tập 6 trang 200 SBT Hình học 11
Bài tập 7 trang 200 SBT Hình học 11
Bài tập 8 trang 200 SBT Hình học 11
Bài tập 9 trang 200 SBT Hình học 11
Bài tập 1 trang 124 SGK Hình học 11 NC
Bài tập 2 trang 124 SGK Hình học 11 NC
Bài tập 3 trang 125 SGK Hình học 11 NC
Bài tập 1 trang 201 SBT Hình học 11
Bài tập 4 trang 125 SGK Hình học 11 NC
Bài tập 5 trang 125 SGK Hình học 11 NC
Bài tập 6 trang 125 SGK Hình học 11 NC
Bài tập 7 trang 125 SGK Hình học 11 NC
Bài tập 8 trang 126 SGK Hình học 11 NC
Bài tập 9 trang 126 SGK Hình học 11 NC
Bài tập 2 trang 201 SBT Hình học 11
Bài tập 3 trang 201 SBT Hình học 11
Bài tập 4 trang 201 SBT Hình học 11
Bài tập 5 trang 201 SBT Hình học 11
Bài tập 6 trang 201 SBT Hình học 11
Bài tập 7 trang 202 SBT Hình học 11
Bài tập 8 trang 202 SBT Hình học 11
Bài tập 9 trang 202 SBT Hình học 11
Bài tập 10 trang 202 SBT Hình học 11
Bài tập 11 trang 202 SBT Hình học 11
Bài tập 12 trang 202 SBT Hình học 11
Bài tập 13 trang 203 SBT Hình học 11
Bài tập 14 trang 203 SBT Hình học 11
Bài tập 15 trang 203 SBT Hình học 11
Bài tập 16 trang 203 SBT Hình học 11
Bài tập 17 trang 203 SBT Hình học 11
Bài tập 18 trang 203 SBT Hình học 11
Bài tập 19 trang 204 SBT Hình học 11
Bài tập 20 trang 204 SBT Hình học 11
Bài tập 21 trang 204 SBT Hình học 11
Bài tập 22 trang 204 SBT Hình học 11
Bài tập 23 trang 204 SBT Hình học 11
Bài tập 24 trang 204 SBT Hình học 11
Bài tập 25 trang 205 SBT Hình học 11
Bài tập 26 trang 205 SBT Hình học 11
Bài tập 27 trang 205 SBT Hình học 11
Bài tập 28 trang 205 SBT Hình học 11
Bài tập 29 trang 205 SBT Hình học 11
Bài tập 30 trang 205 SBT Hình học 11
Bài tập 1 trang 125 SGK Hình học 11
Bài tập 2 trang 125 SGK Hình học 11
Bài tập 3 trang 126 SGK Hình học 11
Bài tập 1 trang 199 SBT Hình học 11
Bài tập 4 trang 126 SGK Hình học 11
Bài tập 5 trang 126 SGK Hình học 11
Bài tập 6 trang 126 SGK Hình học 11
Bài tập 7 trang 126 SGK Hình học 11