Giải bài 6 tr 200 SBT Hình học 11
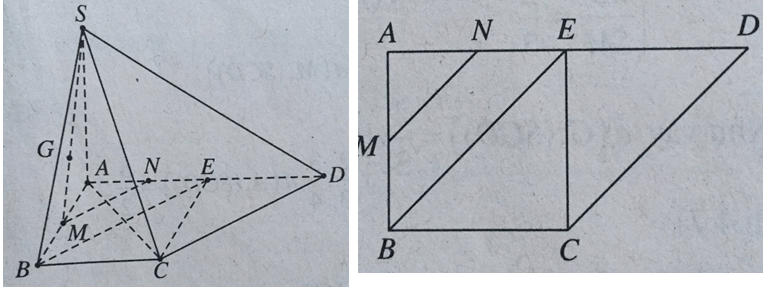
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B với AB = BC = a, AD = 2a. Cạnh bên SA vuông góc với đáy và SC tạo với (SAD) góc 30o. Gọi G là trọng tâm tam giác SAB. Tính khoảng cách từ G đến mặt phẳng (SCD).
Hướng dẫn giải chi tiết
+ Xác định góc của SC với (SAD).
Hạ CE ⊥ AD, ta có E là trung điểm AD và CE ⊥ (SAD) nên \(\widehat {CSE} = {30^0}\).
\(\widehat {CSE}\) cũng chính là góc giữa SC và mp(SAD).
Trong ΔCSE, ta có:
\(SE = CE.\tan {60^0} = a\sqrt 3 \Rightarrow SA = \sqrt {S{E^2} - A{E^2}} = \sqrt {3{a^2} - {a^2}} = a\sqrt 2 \)
Nhận xét:
Gọi M, N lần lượt là trung điểm của AB và AE.
Ta có MN // BE nên MN // CD. Như vậy MN // (SCD). Ta suy ra d(M,(SCD)) = d(N,(SCD)).
Mà \(\frac{{DN}}{{DA}} = \frac{3}{4}\) nên \(d\left( {N,\left( {SCD} \right)} \right) = \frac{3}{4}d\left( {A,\left( {SCD} \right)} \right)\)
+ Xác định khoảng cách từ A đến (SCD).
Vì vậy tam giác ACD vuông cân tại C nên CD vuông góc với AC.
\(\left\{ \begin{array}{l}
CD \bot AC\\
CD \bot SA
\end{array} \right. \Rightarrow CD \bot \left( {SAC} \right) \Rightarrow \left( {SCD} \right) \bot \left( {SAC} \right)\).
Hạ AH ⊥ SC, ta có AH ⊥ (SCD).
Trong tam giác SAC, ta có:
\(\frac{1}{{A{H^2}}} = \frac{1}{{A{S^2}}} + \frac{1}{{A{C^2}}} = \frac{1}{{2{a^2}}} + \frac{1}{{2{a^2}}} = \frac{1}{{{a^2}}} \Rightarrow AH = a\)
Ta có: \(\left\{ \begin{array}{l}
S \in \left( {SCD} \right)\\
\frac{{SG}}{{SM}} = \frac{2}{3}
\end{array} \right.\) nên \(d\left[ {G,\left( {SCD} \right)} \right] = \frac{2}{3}d\left[ {A,\left( {SCD} \right)} \right] = \frac{2}{3}.\frac{3}{4}d\left[ {A,\left( {SCD} \right)} \right] = \frac{a}{2}\)
-- Mod Toán 11 HỌC247
-


Giả sử ta có phép đồng dạng với tỉ số 3 biến hai điểm M và N tương ứng thành M’, N’. Đẳng thức nào sau đây đúng?
bởi Nhật Duy
 16/07/2021
16/07/2021
A. \(M'N' = 3MN\) B. \(MN = 3M'N'\)
C. \(MN = \dfrac{1}{9}M'N'\) D. \(M'N' = \dfrac{1}{3}MN\)
Theo dõi (0) 1 Trả lời -


Cho hình chóp là \(S.ABCD\) có đáy \(ABCD\) là tứ giác lồi. Gọi \(O\) là giao điểm của \(AC\) và \(BD\), \(M\) là giao điểm của \(AB\) và \(CD\), \(N\)là giao điểm của \(AD\) và \(BC\). Giao tuyến của hai mặt phẳng \(\left( {SAB} \right)\)và \(\left( {SCD} \right)\) là?
bởi thủy tiên
 17/07/2021
17/07/2021
A. \(SA\) B. \(SN\) C. \(SM\) D. \(SO\)
Theo dõi (0) 1 Trả lời -


Trong hệ trục tọa độ Oxy, ta cho \(\vec v\left( {3;3} \right)\) và đường tròn \(\left( C \right):{\mkern 1mu} {\mkern 1mu} {\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 9\). Tìm phương trình đường tròn \(\left( {C'} \right)\) là ảnh của \(\left( C \right)\) qua phép tịnh tiến \({T_{\vec v}}.\)
bởi Nguyễn Bảo Trâm
 16/07/2021
16/07/2021
A. \((C'):{\left( {x - 4} \right)^2} + {\left( {y - 1} \right)^2} = 9\)
B. \((C'):{\left( {x - 2} \right)^2} + {\left( {y - 5} \right)^2} = 9\)
C. \((C'):{\left( {x + 4} \right)^2} + {\left( {y + 1} \right)^2} =9\)
D. \((C'):{\left( {x - 4} \right)^2} + {\left( {y - 1} \right)^2} =3.\)
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 5 trang 200 SBT Hình học 11
Bài tập 7 trang 200 SBT Hình học 11
Bài tập 8 trang 200 SBT Hình học 11
Bài tập 9 trang 200 SBT Hình học 11
Bài tập 1 trang 124 SGK Hình học 11 NC
Bài tập 2 trang 124 SGK Hình học 11 NC
Bài tập 3 trang 125 SGK Hình học 11 NC
Bài tập 1 trang 201 SBT Hình học 11
Bài tập 4 trang 125 SGK Hình học 11 NC
Bài tập 5 trang 125 SGK Hình học 11 NC
Bài tập 6 trang 125 SGK Hình học 11 NC
Bài tập 7 trang 125 SGK Hình học 11 NC
Bài tập 8 trang 126 SGK Hình học 11 NC
Bài tập 9 trang 126 SGK Hình học 11 NC
Bài tập 2 trang 201 SBT Hình học 11
Bài tập 3 trang 201 SBT Hình học 11
Bài tập 4 trang 201 SBT Hình học 11
Bài tập 5 trang 201 SBT Hình học 11
Bài tập 6 trang 201 SBT Hình học 11
Bài tập 7 trang 202 SBT Hình học 11
Bài tập 8 trang 202 SBT Hình học 11
Bài tập 9 trang 202 SBT Hình học 11
Bài tập 10 trang 202 SBT Hình học 11
Bài tập 11 trang 202 SBT Hình học 11
Bài tập 12 trang 202 SBT Hình học 11
Bài tập 13 trang 203 SBT Hình học 11
Bài tập 14 trang 203 SBT Hình học 11
Bài tập 15 trang 203 SBT Hình học 11
Bài tập 16 trang 203 SBT Hình học 11
Bài tập 17 trang 203 SBT Hình học 11
Bài tập 18 trang 203 SBT Hình học 11
Bài tập 19 trang 204 SBT Hình học 11
Bài tập 20 trang 204 SBT Hình học 11
Bài tập 21 trang 204 SBT Hình học 11
Bài tập 22 trang 204 SBT Hình học 11
Bài tập 23 trang 204 SBT Hình học 11
Bài tập 24 trang 204 SBT Hình học 11
Bài tập 25 trang 205 SBT Hình học 11
Bài tập 26 trang 205 SBT Hình học 11
Bài tập 27 trang 205 SBT Hình học 11
Bài tập 28 trang 205 SBT Hình học 11
Bài tập 29 trang 205 SBT Hình học 11
Bài tập 30 trang 205 SBT Hình học 11
Bài tập 1 trang 125 SGK Hình học 11
Bài tập 2 trang 125 SGK Hình học 11
Bài tập 3 trang 126 SGK Hình học 11
Bài tập 1 trang 199 SBT Hình học 11
Bài tập 4 trang 126 SGK Hình học 11
Bài tập 5 trang 126 SGK Hình học 11
Bài tập 2 trang 199 SBT Hình học 11
Bài tập 6 trang 126 SGK Hình học 11
Bài tập 7 trang 126 SGK Hình học 11