Bài tập 9 trang 126 SGK Hình học 11 NC

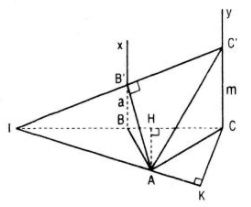
Ta có: 

\(\begin{array}{l}
A{C^2} = 3{a^2},AB{'^2} = 2{a^2}\\
AC{'^2} = 3{a^2} + {m^2},
\end{array}\)

\(B'C'^2= 4{a^2} + {\left( {m - a} \right)^2}\)

a. Tam giác AB’C’ vuông ở A khi và chỉ khi :

\(5{a^2} + {m^2} - 2ma = 2{a^2} + 3{a^2} + {m^2}\)

Vậy tam giác AB’C’ vuông ở A khi và chỉ khi m = 0

Vậy tam giác AB’C’ vuông ở C’ khi và chỉ khi :

\(2{a^2} = 3{a^2} + {m^2} + 4{a^2} + {\left( {m - a} \right)^2}\)

(điều này không xảy ra)

Tam giác AB’C’ vuông ở B’ khi và chỉ khi :

\(\begin{array}{l}
2{a^2} + 4{a^2} + {\left( {m - a} \right)^2} = 3{a^2} + {m^2}\\
 \Leftrightarrow m = 2a
\end{array}\)

Vậy tam giác AB’C’ vuông ở B’ khi và chỉ khi m = 2a

b. Giả sử tam giác AB’C’ vuông ở B’, tức là m = 2a

Vì AH ⊥ BC nên \({a^2} \Rightarrow BH = \frac{a}{2}\)

Từ đó \(HC = \frac{{3a}}{2}\) 

Và \(B'{H^2} = {a^2} + \frac{{{a^2}}}{4} = \frac{{5{a^2}}}{4}\)

\(C'{H^2} = \frac{{9{a^2}}}{4} + 4{a^2} = \frac{{25{a^2}}}{4};B'{C^{\prime 2}} = 5{a^2}\)

Như vậy : ${\mathrm{\backslash (B\text{'}\{H^2\}\; +\; B\text{'}\{C^\{\backslash prime\; 2\}\}\; =\; C\text{'}\{H^2\}\backslash )}}^{}$,

tức là tam giác B’C’H vuông tại B’

Tính góc giữa mp(ABC) và mp(AB’C’) khi m = 2a.

Gọi I là giao điểm của B’C’ và BC. Do BB’ // CC’ , BB’ = a, CC’ = 2a nên BC = BI, B’C’ = B’I.

Xét phép chiếu lên mp(ABC). Ta có tam giác AIC là hình chiếu của tam giác AIC’. Gọi φ là góc giữa mp(ABC) và mp(AB’C’) thì \({S_{AIC}} = {S_{AIC'}}\cos \varphi \)

Ta có: \({S_{AIC}} = 2{S_{ABC}} = {a^2}\sqrt 3 \)

Mặt khác : 

\(\begin{array}{l}
{S_{AIC'}} = \frac{1}{2}IC'.AB'\\
 = \frac{1}{2}.2a\sqrt 5 .a\sqrt 2  = {a^2}\sqrt {10} 
\end{array}\)

Từ đó : \(\cos \varphi  = \frac{{{a^2}\sqrt 3 }}{{{a^2}\sqrt {10} }} = \frac{{\sqrt {30} }}{{10}}\)

Vậy góc giữa mp(ABC) và mp(AB’C’) là φ được tính bởi 

${\backslash (\backslash cos\; \backslash varphi \; =\; \backslash frac\{\{\backslash sqrt\; \{30\}\; \}\}\{\{10\}\},\{0^\; \backslash circ\; \}\; <\; \backslash varphi \; <\; \{90^\; \backslash circ\; \}\backslash )}^{}$

-- Mod Toán 11 HỌC247