Giải bài 5 tr 200 SBT Hình học 11
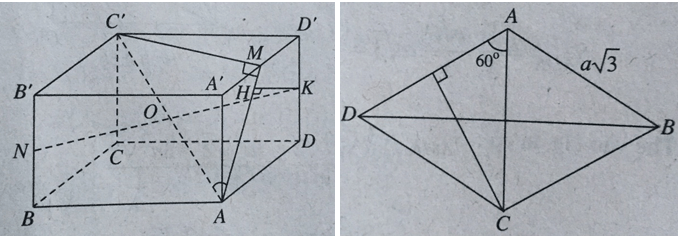
Cho lăng trụ ABCD.A'B'C'D' có đáy ABCD là hình thoi, \(AB = a\sqrt 3 ,\widehat {BAD} = {120^0}\). Góc giữa đường thẳng AC' và mặt phẳng (ADD'A') là 30o. Gọi M là trung điểm A'D', N là trung điểm BB'. Tính khoảng cách từ N đến mặt phẳng (C'MA)
Hướng dẫn giải chi tiết
Nhận xét:
Do tam giác A’B’D’ là tam giác đều nên C’M ⊥ A’D’
(C'A'D') ⊥ (AA'D'D) & (C'A'D') ∩(AA'D'D) ⇒ C’M ⊥ (AA’D’D)
Nên ∠(AC',(AA'D'D)) = ∠(C'AM) = 30o.
Gọi K là trung điểm của DD’, ta có AKC’N là hình bình hành nên K với N đối xứng nhau qua trung điểm O của AC’. Mà O ∈ (AMC’), do đó: d[N,(C'MA)] = d[K,(C'MA)]
+ Xác định khoảng cách từ K đến (C’MA).
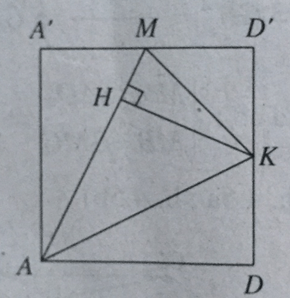
Do (C’MA) vuông góc với (AA’D’D) theo giao tuyến AM nên kẻ KH ⊥ AM, ta có KH ⊥ (C’MA) hay d[K,(C'MA)] = KH.
+ Tính KH.
Ta có: SAMK = SAA'D'D – (SAA'M + SMD'K + SADK) (1)
Trong tam giác AMC’, ta có: \(AM = C'M.\cot {30^0} = \frac{{3a\sqrt 3 }}{2}\).
Trong tam giác AA’M, ta có: \(AA' = \sqrt {A{M^2} - A'{M^2}} = a\sqrt 6 \).
Ta có:
\(\begin{array}{l}
{S_{AA'D'D}} = a\sqrt 6 .a\sqrt 3 = 3{a^2}\sqrt 2 \\
{S_{AA'M}} = \frac{1}{2}a\sqrt 6 .\frac{{a\sqrt 3 }}{2} = \frac{{3{a^2}\sqrt 2 }}{4}\\
{S_{ADK}} = \frac{1}{2}.\frac{{a\sqrt 6 }}{2}.a\sqrt 3 = \frac{{3{a^2}\sqrt 2 }}{4}\\
{S_{MD'K}} = \frac{1}{2}.\frac{{a\sqrt 6 }}{2}.\frac{{a\sqrt 3 }}{2} = \frac{{3a\sqrt 2 }}{8}
\end{array}\)
Thế vào (1), ta có: \({S_{AMK}} = \frac{{9{a^2}\sqrt 2 }}{8}\)
Mà \({S_{AMK}} = \frac{1}{2}AM.HK\) nên \(HK = \frac{{2{S_{AMK}}}}{{AM}} = \frac{{a\sqrt 6 }}{2}\)
Vậy \(d\left[ {N,\left( {C'MA} \right)} \right] = d\left[ {K,\left( {C'MA} \right)} \right] = \frac{{a\sqrt 6 }}{2}\)
-- Mod Toán 11 HỌC247
-


Ở trong không gian cho hai đường thẳng \(CC'\) và \(b\) lần lượt có vectơ chỉ phương là \(\overrightarrow u ,\,\,\overrightarrow v \). Gọi \(\alpha \) là góc giữa hai đường thẳng \(a\) và \(b\). Khẳng định nào sau đây là đúng:
bởi Mai Anh
 17/07/2021
17/07/2021
A. \(\cos \alpha = \cos \left( {\overrightarrow u ;\overrightarrow v } \right)\)
B. \(\overrightarrow u .\overrightarrow v = \sin \alpha \).
C. \(\alpha = \left| {\left( {\overrightarrow u ,\overrightarrow v } \right)} \right|\)
D. \(\cos \alpha = \left| {\cos \left( {\overrightarrow u ,\overrightarrow v } \right)} \right|\)
Theo dõi (0) 1 Trả lời -


Ở trong không gian cho đường thẳng \(\Delta \) và điểm \(O\). Qua \(O\) có bao nhiêu đường thẳng vuông góc với \(\Delta \)?
bởi Lê Vinh
 17/07/2021
17/07/2021
A. 1. B. Vô số. C. 2. D. 3.
Theo dõi (0) 1 Trả lời -


Cho hình chóp \(S.ABC\). Đáy \(ABC\) là tam giác vuông cân tại \(B,\,\,AC = 2a\). Có đường thẳng \(SA\) vuông góc với mặt phẳng \(\left( {ABC} \right)\), \(SA = a\). Khi đó, có cosin của góc tạo bởi \(SC\) và mặt phẳng \(\left( {SAB} \right)\) có giá trị là:
bởi Tuấn Tú
 17/07/2021
17/07/2021
A. \(\dfrac{{\sqrt {15} }}{5}\) B. \(\sqrt {\dfrac{2}{5}} \)
C. \(\sqrt {\dfrac{2}{3}} \) D. \(\dfrac{1}{{\sqrt 3 }}\)
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 6 trang 200 SBT Hình học 11
Bài tập 7 trang 200 SBT Hình học 11
Bài tập 8 trang 200 SBT Hình học 11
Bài tập 9 trang 200 SBT Hình học 11
Bài tập 1 trang 124 SGK Hình học 11 NC
Bài tập 2 trang 124 SGK Hình học 11 NC
Bài tập 3 trang 125 SGK Hình học 11 NC
Bài tập 1 trang 201 SBT Hình học 11
Bài tập 4 trang 125 SGK Hình học 11 NC
Bài tập 5 trang 125 SGK Hình học 11 NC
Bài tập 6 trang 125 SGK Hình học 11 NC
Bài tập 7 trang 125 SGK Hình học 11 NC
Bài tập 8 trang 126 SGK Hình học 11 NC
Bài tập 9 trang 126 SGK Hình học 11 NC
Bài tập 2 trang 201 SBT Hình học 11
Bài tập 3 trang 201 SBT Hình học 11
Bài tập 4 trang 201 SBT Hình học 11
Bài tập 5 trang 201 SBT Hình học 11
Bài tập 6 trang 201 SBT Hình học 11
Bài tập 7 trang 202 SBT Hình học 11
Bài tập 8 trang 202 SBT Hình học 11
Bài tập 9 trang 202 SBT Hình học 11
Bài tập 10 trang 202 SBT Hình học 11
Bài tập 11 trang 202 SBT Hình học 11
Bài tập 12 trang 202 SBT Hình học 11
Bài tập 13 trang 203 SBT Hình học 11
Bài tập 14 trang 203 SBT Hình học 11
Bài tập 15 trang 203 SBT Hình học 11
Bài tập 16 trang 203 SBT Hình học 11
Bài tập 17 trang 203 SBT Hình học 11
Bài tập 18 trang 203 SBT Hình học 11
Bài tập 19 trang 204 SBT Hình học 11
Bài tập 20 trang 204 SBT Hình học 11
Bài tập 21 trang 204 SBT Hình học 11
Bài tập 22 trang 204 SBT Hình học 11
Bài tập 23 trang 204 SBT Hình học 11
Bài tập 24 trang 204 SBT Hình học 11
Bài tập 25 trang 205 SBT Hình học 11
Bài tập 26 trang 205 SBT Hình học 11
Bài tập 27 trang 205 SBT Hình học 11
Bài tập 28 trang 205 SBT Hình học 11
Bài tập 29 trang 205 SBT Hình học 11
Bài tập 30 trang 205 SBT Hình học 11
Bài tập 1 trang 125 SGK Hình học 11
Bài tập 2 trang 125 SGK Hình học 11
Bài tập 3 trang 126 SGK Hình học 11
Bài tập 1 trang 199 SBT Hình học 11
Bài tập 4 trang 126 SGK Hình học 11
Bài tập 5 trang 126 SGK Hình học 11
Bài tập 2 trang 199 SBT Hình học 11
Bài tập 6 trang 126 SGK Hình học 11
Bài tập 7 trang 126 SGK Hình học 11