Giải bài 3 tr 199 SBT Hình học 11
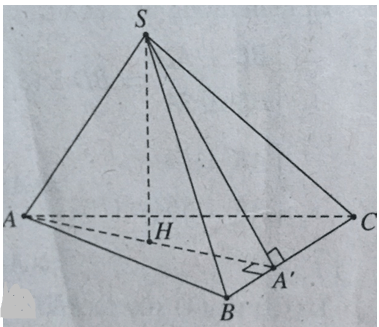
Cho tứ diện SABC có SA, SB, SC vuông góc với nhau từng đôi một. Gọi H là hình chiếu vuông góc của S lên mp(ABC).
a) Chứng minh rằng H là trực tâm của tam giác ABC.
b) Chứng minh rằng \(\frac{1}{{S{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{S{B^2}}} + \frac{1}{{S{C^2}}}\)
c) Chứng minh rằng (SSBC)2 = (SHBC). (SABC) và (SABC)2 = (SSAB)2 + (SSBC)2 + (SSCA)2
d) Chứng minh rằng \(S{G^2} = \frac{{S{A^2} + S{B^2} + S{C^2}}}{9}\) (G là trọng tâm của tam giác ABC) và (AB + BC + CA)2 ≤ 6(SA2 + SB2 + SC2).
e) Chứng minh rằng tam giác ABC có ba góc nhọn và SA2tanA = SB2tanB = SC2tanC = 2SABC
Hướng dẫn giải chi tiết
a) Ta chứng minh: CH ⊥ AB và AH ⊥ BC
Ta có: AB ⊥ SC (do SH ⊥ (ABC)) và AB ⊥ SH (do SC ⊥ (SAB))
⇒ AB ⊥ (SCH) ⇒ AB ⊥ CH (1)
Tương tự, ta có BC ⊥ (SAH) nên AH ⊥ BC (2)
Từ (1) và (2) cho ta H là trực tâm ΔABC.
b) Giả sử CH kéo dài cắt AB tại C’, ta có
AB ⊥ CC' (do H là trực tâm) và AB ⊥ SC' (do AB ⊥ (SCH))
Trong tam giác SCC’, ta có \(\frac{1}{{S{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{S{B^2}}}\,\,\left( 3 \right)\)
Mà SC’ là đường cao trong tam giác vuông SAB nên \(\frac{1}{{SC{'^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{S{B^2}}}\,\,\left( 4 \right)\)
Từ (3), (4) suy ra \(\frac{1}{{S{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{S{B^2}}} + \frac{1}{{S{C^2}}}\) (5)
c)
\(\begin{array}{l}
{S_{HBC}}.{S_{ABC}} = \left( {\frac{1}{2}HA'.BC} \right).\left( {\frac{1}{2}AA'.BC} \right)\\
= \frac{1}{4}HA'.AA'.B{C^2} = \frac{1}{4}SA{'^2}.B{C^2} = {\left( {\frac{1}{2}SA'.BC} \right)^2} = {\left( {{S_{SBC}}} \right)^2}\,\,\left( 6 \right)
\end{array}\)
Tương tự, ta có (SSCA)2 = SHCA. SABC (7)
(SSAB)2 = SHAB. SABC (8)
Cộng (6), (7), (8) vế theo vế, ta có:
\({\left( {{S_{SBC}}} \right)^2} + {\left( {{S_{SCA}}} \right)^2} + {\left( {{S_{SAB}}} \right)^2} = {S_{ABC}}.\underbrace {\left( {{S_{HBC}} + {S_{HCA}} + {S_{HAB}}} \right)}_{{S_{ABC}}} = {\left( {{S_{ABC}}} \right)^2}\)
d) Với G là trọng tâm \(\Delta ABC\), ta có:
\(\begin{array}{l}
\overrightarrow {SG} = \frac{1}{3}\left( {\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} } \right)\\
\Rightarrow S{G^2} = \frac{1}{9}\left( {\overrightarrow {S{A^2}} + \overrightarrow {S{B^2}} + \overrightarrow {S{C^2}} + 2\overrightarrow {SA} .\overrightarrow {SB} + 2\overrightarrow {SB} .\overrightarrow {SC} + 2\overrightarrow {SC} .\overrightarrow {SA} } \right)\\
= \frac{1}{9}\left( {\overrightarrow {S{A^2}} + \overrightarrow {S{B^2}} + \overrightarrow {S{C^2}} } \right)\left( {do\,\overrightarrow {SA} .\overrightarrow {SB} = \overrightarrow {SB} .\overrightarrow {SC} = \overrightarrow {SC} .\overrightarrow {SA} = 0} \right)
\end{array}\)
Áp dụng bất đẳng thức Cô-si, ta có:
2AB. BC ≤ AB2 + BC2
2CA. AB ≤ CA2 + AB2
2BC. CA ≤ BC2 + CA2
Suy ra (AB + BC + CA)2 = AB2 + BC2 + CA2 + 2(AB.BC + BC.CA + CA.AB)
≤ 3(AB2 + BC2 + CA2)
≤ 3(SA2 + SB2 + SB2 + SC2 + SC2 + SA2)
≤ 6(SA2 + SB2 + SC2).
e) Đặt SA = a, SB = b, SC = c
Trong ΔABC, ta có: \(\cos A = \frac{{A{B^2} + A{C^2} - B{C^2}}}{{2AB.AC}} = \frac{{{a^2}}}{{\sqrt {\left( {{a^2} + {b^2}} \right)\left( {{a^2} + {c^2}} \right)} }} > 0\)
Tương tự cos B > 0, cos C > 0.
Vậy ΔABC có ba góc nhọn.
Mặt khác, ta có: \(S{A^4}{\tan ^2}A = {a^4}\left( {\frac{1}{{{{\cos }^2}A}} - 1} \right) = {a^4}\left[ {\frac{{\left( {{a^2} + {b^2}} \right)\left( {{a^2} + {c^2}} \right)}}{{{a^4}}} - 1} \right]\)
= (a2 + b2)(a2 + c2) - a4 = a2b2 + b2c2 + c2a2
= 4(SSAB2 + SSBC2 + SSCA2) = 4(SABC)2 ⇒ SA2tanA = 2SABC.
Tương tự, ta có: SB2tanB = SC2tanC = 2SABC.
Vậy SA2tanA = SB2tanB = SC2tanC = 2SABC.
-- Mod Toán 11 HỌC247
-


Với tứ diện \(ABCD\) có \(AB = BC = AC = CD = DB = a,\,\,AD = \dfrac{{a\sqrt 3 }}{2}\). Ta gọi \(M\) là trung điểm của \(AB\), điểm \(O\) là tâm đường tròn ngoại tiếp tam giác \(BCD\). Đường thẳng \(AO\) cắt mặt phẳng \(\left( {MCD} \right)\) tại \(G\). Tính diện tích tam giác \(GAD\).
bởi Nguyễn Ngọc Sơn
 17/07/2021
17/07/2021
A. \(\dfrac{{\sqrt 3 {a^2}}}{{32}}\) B. \(\dfrac{{3\sqrt 3 {a^2}}}{{32}}\) C. \(\dfrac{{3\sqrt 3 {a^2}}}{{16}}\) D. \(\dfrac{{\sqrt 3 {a^2}}}{{16}}\)
Theo dõi (0) 1 Trả lời -


Ta cho hai đường tròn bằng nhau \(\left( {I;R} \right)\) và \(\left( {I';R'} \right)\) với tâm \(I\) và \(I'\) phân biệt. Có bao nhiêu phép vị tự biến \(\left( {I;R} \right)\) thành \(\left( {I';R'} \right)\)?
bởi Spider man
 17/07/2021
17/07/2021
A. Vô số B. \(0\) C. \(2\) D. \(1\)
Theo dõi (0) 1 Trả lời -


Ở trong mặt phẳng tọa độ \(Oxy\), phép tịnh tiến theo vectơ \(\overrightarrow v \left( {3; - 2} \right)\) biến đường tròn \(\left( C \right):\,\,{x^2} + {y^2} - 2y = 0\) thành đường tròn \(\left( {C'} \right)\). Tìm tọa độ \(I'\) của đường tròn \(\left( {C'} \right)\).
bởi thủy tiên
 17/07/2021
17/07/2021
A. \(I'\left( {3; - 3} \right)\) B. \(I'\left( { - 3;1} \right)\) C. \(I'\left( {3; - 1} \right)\) D. \(I'\left( { - 3;3} \right)\)
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 5 trang 200 SBT Hình học 11
Bài tập 6 trang 200 SBT Hình học 11
Bài tập 7 trang 200 SBT Hình học 11
Bài tập 8 trang 200 SBT Hình học 11
Bài tập 9 trang 200 SBT Hình học 11
Bài tập 1 trang 124 SGK Hình học 11 NC
Bài tập 2 trang 124 SGK Hình học 11 NC
Bài tập 3 trang 125 SGK Hình học 11 NC
Bài tập 1 trang 201 SBT Hình học 11
Bài tập 4 trang 125 SGK Hình học 11 NC
Bài tập 5 trang 125 SGK Hình học 11 NC
Bài tập 6 trang 125 SGK Hình học 11 NC
Bài tập 7 trang 125 SGK Hình học 11 NC
Bài tập 8 trang 126 SGK Hình học 11 NC
Bài tập 9 trang 126 SGK Hình học 11 NC
Bài tập 2 trang 201 SBT Hình học 11
Bài tập 3 trang 201 SBT Hình học 11
Bài tập 4 trang 201 SBT Hình học 11
Bài tập 5 trang 201 SBT Hình học 11
Bài tập 6 trang 201 SBT Hình học 11
Bài tập 7 trang 202 SBT Hình học 11
Bài tập 8 trang 202 SBT Hình học 11
Bài tập 9 trang 202 SBT Hình học 11
Bài tập 10 trang 202 SBT Hình học 11
Bài tập 11 trang 202 SBT Hình học 11
Bài tập 12 trang 202 SBT Hình học 11
Bài tập 13 trang 203 SBT Hình học 11
Bài tập 14 trang 203 SBT Hình học 11
Bài tập 15 trang 203 SBT Hình học 11
Bài tập 16 trang 203 SBT Hình học 11
Bài tập 17 trang 203 SBT Hình học 11
Bài tập 18 trang 203 SBT Hình học 11
Bài tập 19 trang 204 SBT Hình học 11
Bài tập 20 trang 204 SBT Hình học 11
Bài tập 21 trang 204 SBT Hình học 11
Bài tập 22 trang 204 SBT Hình học 11
Bài tập 23 trang 204 SBT Hình học 11
Bài tập 24 trang 204 SBT Hình học 11
Bài tập 25 trang 205 SBT Hình học 11
Bài tập 26 trang 205 SBT Hình học 11
Bài tập 27 trang 205 SBT Hình học 11
Bài tập 28 trang 205 SBT Hình học 11
Bài tập 29 trang 205 SBT Hình học 11
Bài tập 30 trang 205 SBT Hình học 11
Bài tập 1 trang 125 SGK Hình học 11
Bài tập 2 trang 125 SGK Hình học 11
Bài tập 3 trang 126 SGK Hình học 11
Bài tập 1 trang 199 SBT Hình học 11
Bài tập 4 trang 126 SGK Hình học 11
Bài tập 5 trang 126 SGK Hình học 11
Bài tập 2 trang 199 SBT Hình học 11
Bài tập 6 trang 126 SGK Hình học 11