Phần hướng dẫn giải bài tập Toán 10 Chương 2 Bài 1 Hàm số sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng các giải bài tập từ SGK Đại số 10 Cơ bản và Nâng cao.
-
Bài tập 1 trang 38 SGK Đại số 10
Tìm tập xác định của các hàm số sau:
a) \(y= \frac{3x-2}{2x+1};\)
b) \(y= \frac{x-1}{x^{2}+2x-3};\)
c) \(y= \sqrt{2x+1}-\sqrt{3-x}.\)
-
Bài tập 2 trang 38 SGK Đại số 10
Cho hàm số \(y = \left\{ \begin{array}{l}
x + 1,{\rm{ }}x \ge 2\\
{x^2} - 2,{\rm{ }}x < 2
\end{array} \right.\)Tính giá trị của hàm số tại \(x = 3, x = - 1, x = 2\).
-
Bài tập 3 trang 38 SGK Đại số 10
Cho hàm số \(y = 3 x^2 - 2x + 1\). Các điểm sau có thuộc đồ thị hay không?
a) M (- 1;6);
b) N (1;1);
c) P(0;1).
-
Bài tập 4 trang 39 SGK Đại số 10
Xét tính chẵn lẻ của hàm số:
a) \(y = |x|\);
b) \(y = (x + 2)^2\)
c) \(y = x^3 + x\) ;
d) \(y = x^2 + x + 1\).
-
Bài tập 2.1 trang 29 SBT Toán 10
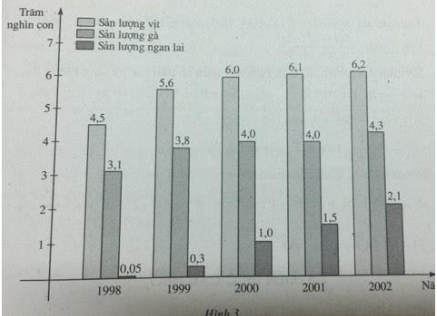
Biểu đồ sau (h.3) biểu thị sản lượng vịt, gà và ngan lai qua 5 năm của một trang trại. Coi y = f(x), y = g(x) và y = h(x) tương ứng là các hàm số biểu thị sự phụ thuộc số vịt, số gà và số ngan lai vào thời gian xx. Qua biểu đồ, hãy:
a) Tìm tập xác định của mỗi hàm số đã nêu.
b) Tìm các giá trị f(2002),g(1999), h(2000)và nêu ý nghĩa của chúng;
c) Tìm hiệu h(2002) – h(1999) và nêu ý nghĩa của nó.
-
Bài tập 2.2 trang 29 SBT Toán 10
Tìm tập xác định của các hàm số
a) \(y = - {x^5} + 7x - 2\)
b) \(y = \frac{{3x + 2}}{{x - 4}}\)
c) \(y = \sqrt {4x + 1} - \sqrt { - 2x + 1} \)
d) \(y = \frac{{2x + 1}}{{\left( {2x + 1} \right)\left( {x - 3} \right)}}\)
-
Bài tập 2.3 trang 30 SBT Toán 10
Cho hàm số
\(y = f\left( x \right) = \left\{ \begin{array}{l}
\frac{{2x - 3}}{{x - 1}},\,\,\,\,\,\,\,x \le 0\\
- {x^2} + 2x,\,\,\,x > 0
\end{array} \right.\)Tính giá trị của hàm số đó tại x = 5; x = −2; x = 0; x = 2.
-
Bài tập 2.4 trang 30 SBT Toán 10
Cho các hàm số :
\(\begin{array}{l}
f\left( x \right) = {x^2} + 2 + \sqrt {2 - x} ;g\left( x \right) = - 2{x^2} - 3x + 5;\\
u\left( x \right) = \left\{ \begin{array}{l}
\sqrt {3 - x} ,\,\,\,\,x < 2\\
\sqrt {{x^2} - 4} ,\,\,x \ge 2
\end{array} \right.;v\left( x \right) = \left\{ \begin{array}{l}
\sqrt {6 - x} ,\,\,\,x \le 0\\
{x^2} + 1,\,\,\,\,\,x > 0
\end{array} \right.
\end{array}\)Tính các giá trị \(f\left( { - 2} \right) - f\left( 1 \right);g\left( 3 \right);f\left( { - 7} \right) - g\left( { - 7} \right)\)
\(f\left( { - 1} \right) - u\left( { - 1} \right);u\left( 3 \right) - v\left( 3 \right);v\left( 0 \right) - g\left( 0 \right);\frac{{f\left( 2 \right) - f\left( { - 2} \right)}}{{v\left( 2 \right) - v\left( { - 3} \right)}}\)
-
Bài tập 2.5 trang 31 SBT Toán 10
Xét tính đồng biến, nghịch biến của hàm số trên các khoảng tương ứng
a) y = −2x+3 trên R.
b) y = x2+10x+9 trên (−5;+∞);
c) \(y = - \frac{1}{{x + 1}}\) trên (−3;−2) và (2;3).
-
Bài tập 2.6 trang 31 SBT Toán 10
Xét tính chẵn, lẻ của các hàm số
a) y = −2 ;
b) y = 3x2−1 ;
c) y = −x4+3x−2.
d) \(y = \frac{{ - {x^4} + {x^2} + 1}}{x}\).
-
Bài tập 2.7 trang 31 SBT Toán 10
Tập xác định của hàm số \(y = \frac{{3x + 10}}{{{x^2} + 14x + 45}}\) là
A. R
B. R\{-5;9}
C. R\{-5;- 9}
D. R\{5;9}
-
Bài tập 2.8 trang 31 SBT Toán 10
Hàm số \(y = \sqrt {x + 7} + \frac{2}{{{x^2} + 6x - 16}}\) có tập xác định D bằng
A. (7;+∞)
B. (7;+∞)∖{−8;2}
C. [−7;7]∖{2}
D. [−7;+∞)∖{2}
-
Bài tập 2.9 trang 31 SBT Toán 10
Cho các hàm số \(f\left( x \right) = \left\{ \begin{array}{l}
{x^2} - 1,\,\,\,x \le 3\\
\sqrt {x + 2} ,\,x > 3
\end{array} \right.\)\(g\left( x \right) = \left\{ \begin{array}{l}
2x + 3,\,\,x > 1\\
{x^2} + 2,\,\,x \le 1
\end{array} \right.\)Khi đó giá trị: f(0) + 2f(7) − g(1) bằng:
A. 2 B. 0
C. \(\sqrt 2 + 3\) D. −2
-
Bài tập 1 trang 44 SGK Toán 10 NC
Tìm tập xác định của hàm số sau:
a) \(y = \frac{{3x + 5}}{{{x^2} - x + 1}}\);
b) \(y = \frac{{x - 2}}{{{x^2} - 3x + 2}}\);
c) \(y = \frac{{\sqrt {x - 1} }}{{x - 2}}\);
d) \(y = \frac{{{x^2} - 2}}{{\left( {x + 2} \right)\sqrt {x + 1} }}\)
-
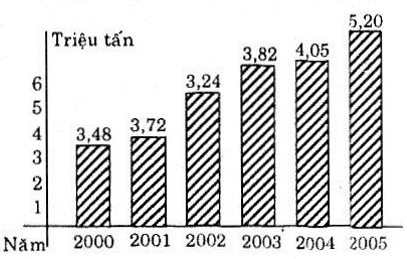
Bài tập 2 trang 44 SGK Toán 10 NC
Biểu đồ ở hình bên cho biết số triệu tấn gạo xuất khẩu của Việt Nam trong các năm từ 2000 đến 2005. Biểu đồ này cho một hàm số. Hãy cho biết tập xác định và nêu một vài giá trị của hàm số đó
-
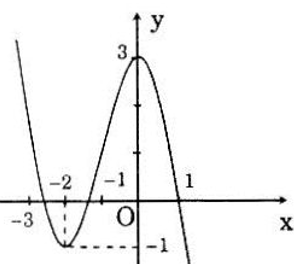
Bài tập 3 trang 45 SGK Toán 10 NC
Hình bên là đồ thị của một hàm số có tập xác định là R. Dựa vào đồ thị hãy lập bảng biến thiên của hàm số
-
Bài tập 4 trang 45 SGK Toán 10 NC
Khảo sát sự biến thiên của mỗi hàm số sau và lập bảng của nó:
a) \(y = x^2 + 2x - 2\) trên mỗi khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( { - 1; + \infty } \right)\);
b) \(y = - 2x^2 + 4x + 1\) trên mỗi khoảng \(\left( { - \infty ; -1} \right)\) và \(\left( { 1; + \infty } \right)\);
c) \(y = \frac{2}{{x - 3}}\) trên mỗi khoảng \(\left( { - \infty ; 3} \right)\) và \(\left( { 3; + \infty } \right)\)
-
Bài tập 5 trang 45 SGK Toán 10 NC
Mỗi hàm số sau là hàm số chẵn hay hàm số lẻ?
a) y = x4 – 3x2 + 1
b) y = - 2x3 + x
c) y = |x + 2| - |x – 2|
d) y = |2x + 1| + |2x – 1|
-
Bài tập 6 trang 45 SGK Toán 10 NC
Cho đường thẳng (d): y = 0,5x. Hỏi ta sẽ được đồ thị của hàm số nào khi tịnh tiến (d):
a) Lên trên 3 đơn vị
b) Xuống dưới 1 đơn vị
c) Sang phải 2 đơn vị
d) Sang trái 6 đơn vị
-
Bài tập 7 trang 45 SGK Toán 10 NC
Quy tắc đặt tương ứng mỗi số thực dương với căn bậc hai của nó có phải là một hàm số không? Vì sao?
-
Bài tập 8 trang 45 SGK Toán 10 NC
Giả sử (G) là đồ thị của hàm số y = f(x) xác định trên tập D; A là một điểm trên trục hoành có hoành độ bằng a. Từ A, dựng đường thẳng (d) song song (hoặc trùng) với trục tung.
a) Khi nào thì (d) có điểm chung với (G).
b) (d) có thể có bao nhiêu điểm chung với (G)? Vì sao?
c) Đường tròn có thể là đồ thị của hàm số không? Vì sao?
-
Bài tập 9 trang 46 SGK Toán 10 NC
Tìm tập xác định của mỗi hàm số sau:
a) \(y = \frac{{3x + 1}}{{{x^2} - 9}}\)
b) \(y = \frac{x}{{1 - {x^2}}} - \sqrt { - x} \)
c) \(y = \frac{{x - 3\sqrt {2 - x} }}{{\sqrt {x + 2} }}\)
d) \(y = \frac{{\sqrt {x - 1} + \sqrt {4 - x} }}{{\left( {x - 2} \right)\left( {x - 3} \right)}}\)
-
Bài tập 10 trang 46 SGK Toán 10 NC
Cho hàm số
\(f\left( x \right) = \left\{ \begin{array}{l}
- 2\left( {x - 2} \right);\,\,\,\,\, - 1 \le x < 1\\
\sqrt {{x^2} - 1} ;\,\,\,\,\,\,\,\,\,\,\,x \ge 1
\end{array} \right.\)a) Tìm tập xác định của hàm số
b) Tính \(f\left( { - 1} \right);f\left( {0,5} \right);f\left( {\frac{{\sqrt 2 }}{2}} \right);\)
\(f\left( 1 \right);f\left( 2 \right)\)
-
Bài tập 11 trang 46 SGK Toán 10 NC
Trong các điểm A(- 2; 8); B(4;12), C(2;8) và \(D\left( {5;25 + \sqrt 2 } \right)\), điểm nào thuộc, điểm nào không thuộc đồ thị hàm số \(f\left( x \right) = {x^2} + \sqrt {x - 3} \)? Vì sao?
-
Bài tập 12 trang 46 SGK Toán 10 NC
Khảo sát sự biến thiên của hàm số sau trên khoảng đã cho :
a) \(y = \frac{1}{{x - 2}}\) trên mỗi khoảng \(\left( { - \infty ;2} \right)\) và (2; + ∞ )
b) y = x2 – 6x + 5 trên mỗi khoảng \(\left( { - \infty ;3} \right)\) và (3; + ∞)
c) y = x2005 + 1 trên khoảng (- ∞; + ∞ )
-
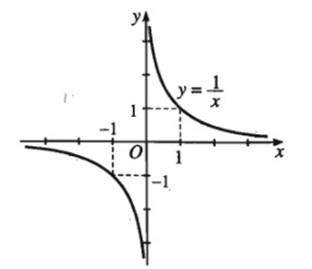
Bài tập 13 trang 46 SGK Toán 10 NC
Hàm số \(y = \frac{1}{x}\) có đồ thị như hình 2.10
a) Dựa vào đồ thị, hãy lập bảng biến thiên của hàm số đó
b) Bằng tính toán, hãy khảo sát sự biến thiên của hàm số trên khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {0; + \infty } \right)\) và kiểm tra lại kết quả so với bảng biến thiên đã lập
-
Bài tập 14 trang 47 SGK Toán 10 NC
Tập con S của tập số thực R gọi là đối xứng nếu mọi x thuộc S, ta đều có – x thuộc S. Em có nhận xét gì về tập xác định của một hàm số chẵn (lẻ).
Từ nhận xét đó, em có kết luận gì về tính chẵn – lẻ của hàm số \(y = \sqrt x \)? Tại sao?
-
Bài tập 15 trang 47 SBT Toán 10 NC
Gọi (d) là đường thẳng y = 2x và (d’) là đường thẳng y = 2x–3. Ta có thể coi (d’) có được là do tịnh tiến (d):
a) Lên trên hay xuống dưới bao nhiêu đơn vị?
b) Sang trái hay sang phải bao nhiêu đơn vị?
-
Bài tập 16 trang 47 SBT Toán 10 NC
Cho đồ thị (H) của hàm số: \(y = - \frac{2}{x}\)
a) Tịnh tiến (H) lên trên 1 đơn vị, ta được đồ thị của hàm số nào?
b) Tịnh tiến (H) sang trái 3 đơn vị, ta được đồ thị của hàm số nào?
c) Tịnh tiến (H) lên trên 1 đơn vị, sau đó tịnh tiến đồ thị nhận được sang trái 3 đơn vị, ta được đồ thị của hàm số nào ?