Bài tập 4 trang 45 SGK Toán 10 NC
Khảo sát sự biến thiên của mỗi hàm số sau và lập bảng của nó:
a) \(y = x^2 + 2x - 2\) trên mỗi khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( { - 1; + \infty } \right)\);
b) \(y = - 2x^2 + 4x + 1\) trên mỗi khoảng \(\left( { - \infty ; -1} \right)\) và \(\left( { 1; + \infty } \right)\);
c) \(y = \frac{2}{{x - 3}}\) trên mỗi khoảng \(\left( { - \infty ; 3} \right)\) và \(\left( { 3; + \infty } \right)\)
Hướng dẫn giải chi tiết
a) Ta có :
+ Với mọi \({x_1};{x_2} \in \left( { - \infty ; - 1} \right)\) và \({x_1} \ne {x_2}\) ta có:
\(f(x_2) – f(x_1) = x_2^2 + 2x_2 – 2 – (x_1^2 + 2x_1 – 2)\)
\(= x_2^2 – x_1^2 + 2(x_2 – x_1) = (x_2 – x_1)(x_1 + x_2 + 2)\)
\( \Rightarrow \frac{{f\left( {{x_2}} \right) - f\left( {{x_1}} \right)}}{{{x_2} - {x_1}}} = {x_1} + {x_2} + 2\)
Vì \(x_1<-1\) và \(x_2<-1\) nên \(x_1+x_2+2<0\) nên \(\frac{{f\left( {{x_2}} \right) - f\left( {{x_1}} \right)}}{{{x_2} - {x_1}}} < 0\)
Vậy hàm số \(y=x^2+2x-2\) nghịch biến trên \(\left( { - \infty ; - 1} \right)\)
+ Với mọi \({x_1};{x_2} \in \left( { - 1; + \infty } \right)\) và \({x_1} \ne {x_2}\) ta có:
\(\frac{{f\left( {{x_2}} \right) - f\left( {{x_1}} \right)}}{{{x_2} - {x_1}}} = {x_1} + {x_2} + 2 > 0\) (vì \(x_1>-1; x_2>-1\)
b) Ta có :
+ Với mọi \({x_1};{x_2} \in \left( { - \infty ; 1} \right)\) và \({x_1} \ne {x_2}\) ta có:
\(f(x_2) – f(x_1) \)
\(= (-2x_2^2 + 4x_2 + 1) – (-2x_1^2 + 4x_1 + 1)\)
\(= -2(x_2^2 - x_1^2) + 4(x_2 - x_1) \)
\(= 2(x_2 - x_1)(2 – x_1 – x_2)\)
\( \Rightarrow \frac{{f\left( {{x_2}} \right) - f\left( {{x_1}} \right)}}{{{x_2} - {x_1}}} = 2\left( {2 - {x_1} - {x_2}} \right)\)
Vì \(x_1 < 1\) và \(x_2 < 1\) nên \(2 - x_1 – x_2 > 0\)
Vậy hàm số \(y = -2x^2 + 4x + 1\) đồng biến trên khoảng \(\left( { - \infty ;1} \right)\)
+ Với mọi \({x_1};{x_2} \in \left( { 1; + \infty } \right)\) và \({x_1} \ne {x_2}\) ta có:
\(\frac{{f\left( {{x_2}} \right) - f\left( {{x_1}} \right)}}{{{x_2} - {x_1}}} = 2\left( {2 - {x_1} - {x_2}} \right) < 0\) (vì \(x_1>1\) và \(x_2>1\))
Vậy hàm số \(y=-2x^2+4x+1\) nghịch biến trên khoảng \(\left( {1; + \infty } \right)\)
c) Ta có :
+ Với mọi \({x_1};{x_2} \in \left( { - \infty ; 3} \right)\) và \({x_1} \ne {x_2}\) ta có:
\(\begin{array}{l}
f\left( {{x_2}} \right) - f\left( {{x_1}} \right) = \frac{2}{{{x_2} - 3}} - \frac{2}{{{x_1} - 3}}\\
= \frac{{2\left( {{x_1} - 3} \right) - 2\left( {{x_2} - 3} \right)}}{{\left( {{x_1} - 3} \right)\left( {{x_2} - 3} \right)}} = \frac{{2\left( {{x_1} - {x_2}} \right)}}{{\left( {{x_1} - 3} \right)\left( {{x_2} - 3} \right)}}
\end{array}\)
\( \Rightarrow \frac{{f\left( {{x_2}} \right) - f\left( {{x_1}} \right)}}{{{x_2} - {x_1}}} = \frac{{ - 2}}{{\left( {{x_1} - 3} \right)\left( {{x_2} - 3} \right)}}\) (vì \(x_1<3; x_2<3\) nên \((x_1-3)(x_2-3)>0\))
\( \Rightarrow \frac{{f\left( {{x_2}} \right) - f\left( {{x_1}} \right)}}{{{x_2} - {x_1}}} < 0\)
Vậy hàm số \(y = \frac{2}{{x - 3}}\) nghịch biến trên \(\left( { - \infty ;3} \right)\)
+ Với mọi \({x_1};{x_2} \in \left( { 3; + \infty } \right)\) và \({x_1} \ne {x_2}\) ta có:
\(\frac{{f\left( {{x_2}} \right) - f\left( {{x_1}} \right)}}{{{x_2} - {x_1}}} = \frac{{ - 2}}{{\left( {{x_1} - 3} \right)\left( {{x_2} - 3} \right)}} < 0\) (vì \(x_1 > 3; x_2 > 3\) nên \((x_1 – 3)(x_2 – 3) > 0\))
Vậy hàm số \(y = \frac{2}{{x - 3}}\) nghịch biến trên \(\left( {3; + \infty } \right)\)
-- Mod Toán 10 HỌC247
-

 Tìm tập xác định của hàm số lớp 10 ạ
Tìm tập xác định của hàm số lớp 10 ạ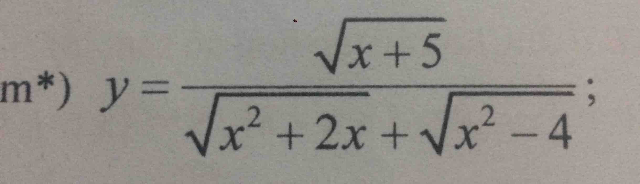 Theo dõi (0) 5 Trả lời
Theo dõi (0) 5 Trả lời -


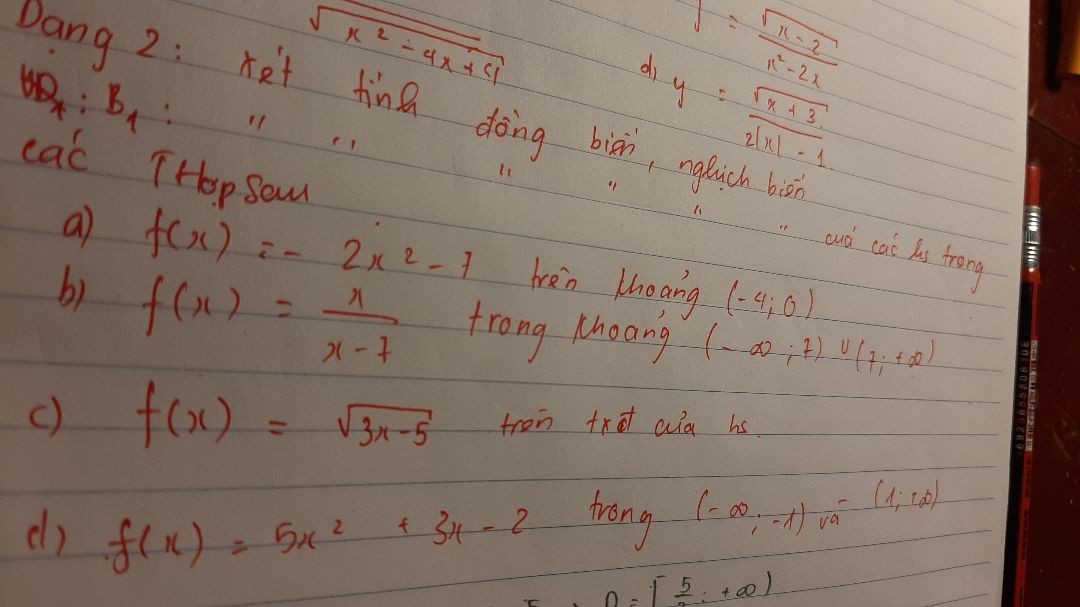 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm tập xác định của hàm số y=2-4x
bởi Bích Dương
 01/10/2019
A> Y=2-4x b> Y=x2 4x 15Theo dõi (0) 0 Trả lời
01/10/2019
A> Y=2-4x b> Y=x2 4x 15Theo dõi (0) 0 Trả lời -


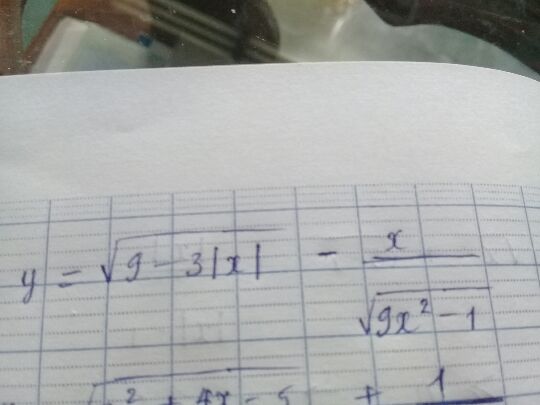 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


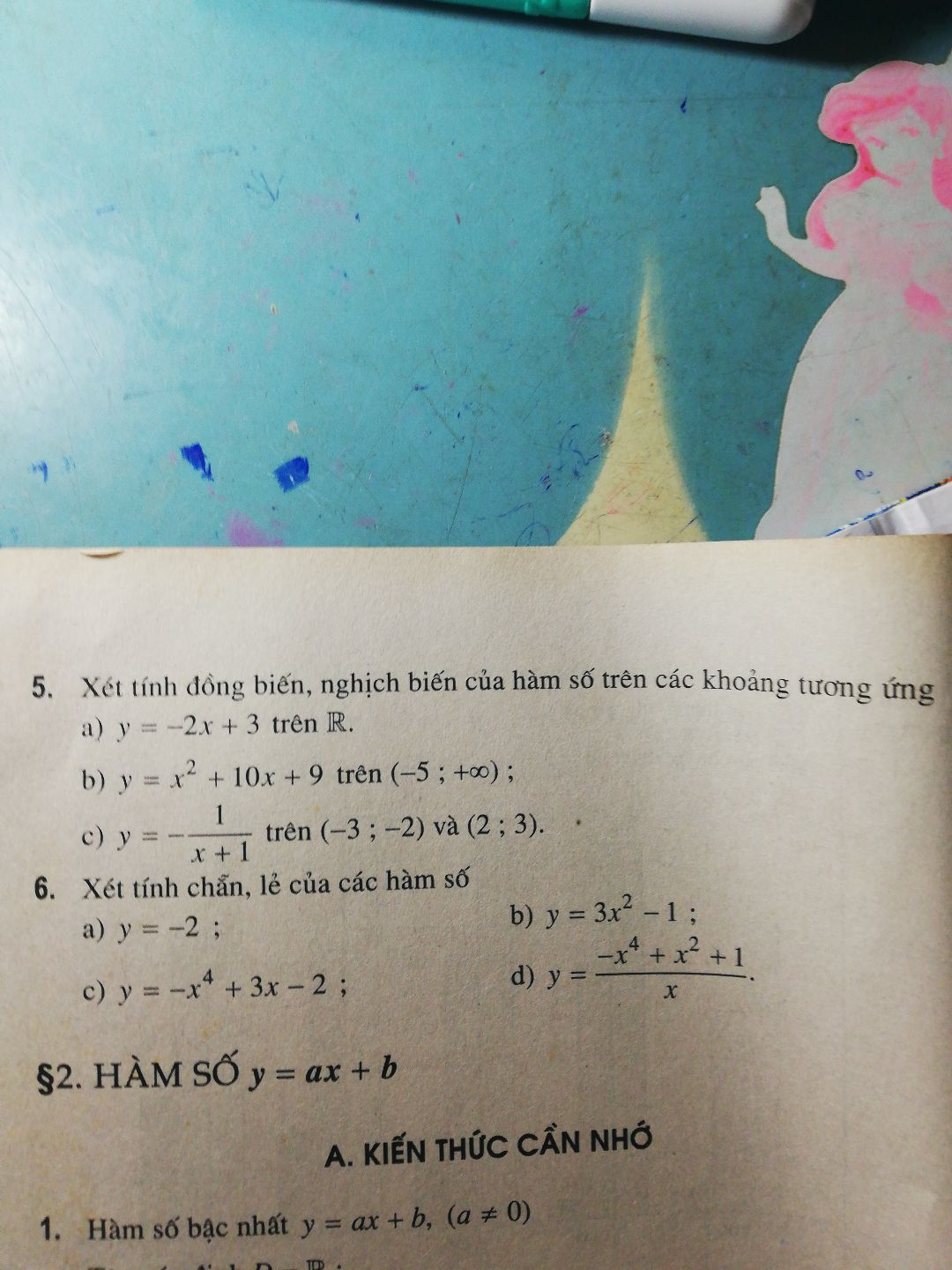 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Nêu cách xác định hàm số chẵn lẻ
bởi Huynh Thi Tuyet Ngan
 15/12/2018
15/12/2018
cách xác định hàm số chẵn lẻ
Theo dõi (0) 3 Trả lời -


Cho f(x) =
có tập xác định Df ; g(x) =
có tập xác định Dg . Tìm m để Dg
Df
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 2 trang 44 SGK Toán 10 NC
Bài tập 3 trang 45 SGK Toán 10 NC
Bài tập 5 trang 45 SGK Toán 10 NC
Bài tập 6 trang 45 SGK Toán 10 NC
Bài tập 7 trang 45 SGK Toán 10 NC
Bài tập 8 trang 45 SGK Toán 10 NC
Bài tập 9 trang 46 SGK Toán 10 NC
Bài tập 10 trang 46 SGK Toán 10 NC
Bài tập 11 trang 46 SGK Toán 10 NC
Bài tập 12 trang 46 SGK Toán 10 NC
Bài tập 13 trang 46 SGK Toán 10 NC
Bài tập 14 trang 47 SGK Toán 10 NC





