Bài tập 13 trang 46 SGK Toán 10 NC
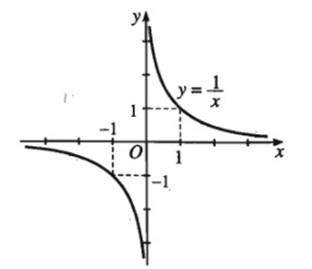
Hàm số \(y = \frac{1}{x}\) có đồ thị như hình 2.10
a) Dựa vào đồ thị, hãy lập bảng biến thiên của hàm số đó
b) Bằng tính toán, hãy khảo sát sự biến thiên của hàm số trên khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {0; + \infty } \right)\) và kiểm tra lại kết quả so với bảng biến thiên đã lập
Hướng dẫn giải chi tiết
a) Bảng biến thiên của hàm số
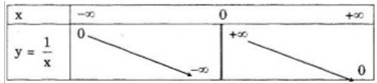
b) Với \({x_1},{x_2} \in \left( { - \infty ;0} \right)\) và \({x_1} \ne {x_2}\) ta có:
\(\frac{{f\left( {{x_2}} \right) - f\left( {{x_1}} \right)}}{{{x_2} - {x_1}}} = \frac{{\frac{1}{{{x_2}}} - \frac{1}{{{x_1}}}}}{{{x_2} - {x_1}}} = \frac{{ - 1}}{{{x_1}{x_2}}} < 0\) (vì \(x_1 < 0; x_2 < 0\))
Vậy hàm số \(y = \frac{1}{x}\) nghịch biến trên \(\left( { - \infty ;0} \right)\)
Tương tự hàm số \(y = \frac{1}{x}\) cũng nghịch biến trên \(\left( {0; + \infty } \right)\)
-- Mod Toán 10 HỌC247
-


Xét sự biến thiên của hàm số y=2x^2 + 4x +1
bởi Nguyễn Chibi'ss
 22/07/2017
22/07/2017
y=2x2 + 4x +1 trên (khoảng từ 1 đến cộng vô cực)
Theo dõi (1) 1 Trả lời





