Giải bài 9 tr 50 sách GK Toán ĐS lớp 10
Khảo sát sự biến thiên và vẽ đồ thị các hàm số sau:
a) \(y = \frac{1}{2}x - 1\) b) \(y = 4 - 2x\)
c) \(y = \sqrt {{x^2}} \) d) \(y = \left| {x + 1} \right|\)
Hướng dẫn giải chi tiết bài 9
Câu a:
Khảo sát sự biến thiên và vẽ đồ thị hàm số \(y = \frac{1}{2}x - 1\)
Hàm số \(y = \frac{1}{2}x - 1\) có tập xác định là R.
Chiều biến thiên: Vì hàm số \(y = \frac{1}{2}x - 1\)là hàm số bậc nhất có hệ số \(a = \frac{1}{2} > 0\) nên hàm số \(y = \frac{1}{2}x - 1\) đồng biến trên khoảng \(( - \infty ; + \infty ).\)
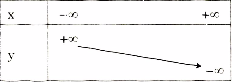
Bảng biến thiên khi x dần tới \( + \infty \) thì \(y = \frac{1}{2}x - 1\) dần tới \( + \infty \), khi x dần tới \( - \infty \) thì \( + \infty \) dần tới \( - \infty \). Ta có bảng biến thiên:

Đồ thị hàm số \(y = \frac{1}{2}x - 1\)
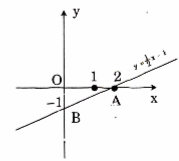
Vì đồ thị hàm số \(y = \frac{1}{2}x - 1\) là một đường thẳng nên ta chỉ việc xác định hai điểm phân biệt thuộc đồ thị, sau đó xác định đường thẳng qua hai điểm đó.
Cho \(x = 0 \Rightarrow y = - 1\)
Cho \(y = 0 \Rightarrow x = 2\)
Vậy đường thẳng qua hai điểm A(2; 0), B(0; -1) chính là đồ thị của hàm số \(y = \frac{1}{2}x - 1\)
Câu b:
\(y = 4 - 2x\)
Tập xác định của hàm số \(y = 4 - 2x\)là \(\mathbb{R}\).
Chiều biến thiên. Vì hàm số đã cho là hàm số bậc nhất có hệ số a = -2 nên hàm số nghịch biến trên khoảng \(( - \infty ; + \infty )\)
Bảng biến thiên: Khi x dần tới \( + \infty \) thì y dần tới \( - \infty \), khi x dần tới \( - \infty \) thì y dần tới \( + \infty \). Ta có bảng biến thiên:
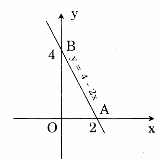
Đồ thị hàm số \(y = 4 - 2x\) là 1 đường thẳng đi qua hai điểm: A(2; 0); B(0; 4)
Đồ thị ở hình bên:
Câu c:
Hàm số \(y = \sqrt {{x^2}} \)có thể viết dưới dạng \(y = |x|\)
Tập xác định của hàm số \(y = |x|\) là tập \(\mathbb{R}\)
Chiều biến thiên:
Theo định nghĩa có giá trị tuyệt đối, ta có:
\(y = |x| = \left\{ \begin{array}{l}x\,\,\,\,\,\,neu\,\,x \ge 0\\ - x\,\,\,neu\,\,x < 0\end{array} \right.\)
Từ đó ta có: Hàm số\(y = |x|\)đồng biến trên khoảng \((0; + \infty )\) và nghịch biến trên khoảng \(( - \infty ; + 0)\)
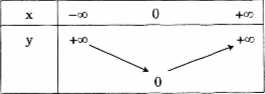
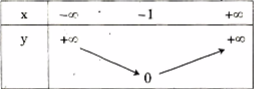
Bảng biến thiên: khi x > 0 và x dần tới \( + \infty \) thì y = x dần tới \( + \infty \). Khi x < 0 và dần tới \( - \infty \) thì y = -x dần tới \( + \infty \). Ta có bảng biến sau đây:
Đồ thị:
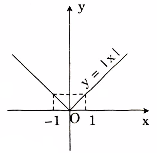
Trong nửa khoảng \({\rm{[}}0; + \infty )\) đồ thị của hàm số \(y = |x|\) trùng với đồ thị hàm số y = x (phần bên phải Oy)
Đồ thị có hình dạng sau:
Chú ý: Vì \(y = |x|\) là hàm số chẵn nên đồ thị của nó đối xứng qua trục tung.
Câu d:
Hàm số \(y = |x + 1|\) có thể viết dưới dạng:
\(y = \left\{ \begin{array}{l}x + 1\,\,\,\,\,\,\,\,\,\,\,\,\,neu\,\,\,x \ge - 1\\ - x - 1\,\,\,\,\,\,\,\,\,neu\,\,\,x < - 1\end{array} \right.\,\,\,\,\,\,\,\,(*)\)
Tập xác định của hàm số \(y = |x + 1|\) là tập \(\mathbb{R}\)
Chiều biến thiên: Từ cách viết hàm số đã cho dưới dạng (*), ta có hàm số \(y = |x + 1|\) đồng biến trên khoảng \(( - 1; + \infty )\) và nghịch biến trên khoảng \(( - \infty ; - 1).\)
Bảng biến thiên: Khi x > - 1 và x dần tới \( + \infty \) thì y dần tới \( + \infty \).
Khi x < - 1 và x dần tới y = -x – 1 dần tới \( + \infty \). Ta có bảng biến thiên
Đồ thị

Trên nửa khoảng \({\rm{[}} - 1; + \infty )\) đồ thị của hàm số y = |x + 1| là đồ thị của hàm số y = x + 1.
Trên khoảng \(( - \infty ; - 1)\) đồ thị của hàm số y = |x + 1|là đồ thị của hàm số y = -x – 1.
-- Mod Toán 10 HỌC247
-


Với những giá trị nào của m thì hàm số \(y = - {x^3} + 3({m^2} - 1){x^2} + 3x\) là hàm số lẻ:
bởi Bao Chau
 22/01/2021
22/01/2021
A. m = 1
B. m = -1
C. m = ±1
D. Kết quả khác.
Theo dõi (0) 1 Trả lời -


ho đồ thị hàm số y = f(x) như hình vẽ
bởi hà trang
 21/01/2021
21/01/2021
.png)
Kết luận nào trong các kết luận sau là đúng:
A. Đồng biến trên R
B. Hàm số chẵn
C. Hàm số lẻ
D. Cả ba đáp án đếu sai
Theo dõi (0) 1 Trả lời -


Cho hàm số y = f(x), y = g(x) có cùng tập xác định D. Chứng minh rằng: Nếu hai hàm số trên một chẵn một lẻ thì hàm số y = f(x).g(x) là hàm số lẻ
bởi Hoang Vu
 21/01/2021
Theo dõi (0) 1 Trả lời
21/01/2021
Theo dõi (0) 1 Trả lời -


Cho hàm số y = f(x), y = g(x) có cùng tập xác định D. Chứng minh rằng: Nếu hai hàm số trên lẻ thì hàm số y = f(x) + g(x) là hàm số lẻ
bởi Phung Thuy
 22/01/2021
Theo dõi (0) 1 Trả lời
22/01/2021
Theo dõi (0) 1 Trả lời -


Parabol \(y = a{x^2} + bx + 2\) đi qua hai điểm M(1;5) và N(-2;8) có phương trình là:
bởi Lê Bảo An
 30/05/2020
Theo dõi (0) 1 Trả lời
30/05/2020
Theo dõi (0) 1 Trả lời -


Hình vẽ bên là đồ thị của hàm số nào?
bởi Trần Bảo Việt
 30/05/2020
30/05/2020
A. \(y = - {\left( {x + 1} \right)^2}\).
B. \(y = - {\left( {x - 1} \right)^2}\).
C. \(y = {\left( {x + 1} \right)^2}\).
D. \(y = {\left( {x -1} \right)^2}\).
Theo dõi (0) 1 Trả lời -


Cho hàm số: \(y = {x^2} - 2x + 3\). Trong các mệnh đề sau, tìm mệnh đề đúng?
bởi Lê Gia Bảo
 31/05/2020
31/05/2020
A. y tăng trên \(\left( {0; + \infty } \right)\).
B. y giảm trên \(\left( { - \infty ;2} \right)\).
C. Đồ thị của y có đỉnh I(1;0).
D. y tăng trên \(\left( {2; + \infty } \right)\).
Theo dõi (0) 1 Trả lời -


Hàm số nào sau đây nghịch biến trong khoảng \(\left( { - \infty ;0} \right)\)?
bởi Mai Bảo Khánh
 30/05/2020
30/05/2020
A. \(y = \sqrt 2 {x^2} + 1\) .
B. \(y =- \sqrt 2 {x^2} + 1\) .
C. \(y = \sqrt 2 {\left( {x + 1} \right)^2}\) .
D. \(y = -\sqrt 2 {\left( {x + 1} \right)^2}\)
Theo dõi (0) 1 Trả lời -


Cho hàm số \(y = f\left( x \right) = - {x^2} + 4x + 2\). Mệnh đề nào sau đây là đúng?
bởi Nguyễn Sơn Ca
 31/05/2020
31/05/2020
A. y giảm trên \(\left( {2; + \infty } \right)\).
B. y giảm trên \(\left( { - \infty ;2} \right)\).
C. y tăng trên \(\left( {2; + \infty } \right)\).
D. y tăng trên \(\left( { - \infty ; + \infty } \right)\).
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 7 trang 50 SGK Đại số 10
Bài tập 8 trang 50 SGK Đại số 10
Bài tập 10 trang 51 SGK Đại số 10
Bài tập 11 trang 51 SGK Đại số 10
Bài tập 12 trang 51 SGK Đại số 10
Bài tập 2.27 trang 42 SBT Toán 10
Bài tập 2.28 trang 42 SBT Toán 10
Bài tập 2.29 trang 43 SBT Toán 10
Bài tập 2.30 trang 43 SBT Toán 10
Bài tập 2.31 trang 43 SBT Toán 10
Bài tập 2.32 trang 43 SBT Toán 10
Bài tập 2.33 trang 43 SBT Toán 10
Bài tập 39 trang 63 SGK Toán 10 NC
Bài tập 40 trang 63 SGK Toán 10 NC
Bài tập 41 trang 63 SGK Toán 10 NC
Bài tập 42 trang 63 SGK Toán 10 NC
Bài tập 43 trang 63 SGK Toán 10 NC
Bài tập 44 trang 64 SGK Toán 10 NC




.PNG)

