Bài tập 44 trang 64 SGK Toán 10 NC

a) Ta có 

\(y = \left\{ \begin{array}{l}
\frac{3}{2}x - 2,\,\,\,\,\,\,\,x \ge \frac{3}{4}\\
 - \frac{3}{2}x + 2,\,\,\,\,x < \frac{3}{4}
\end{array} \right.\)

Đồ thị hàm số 

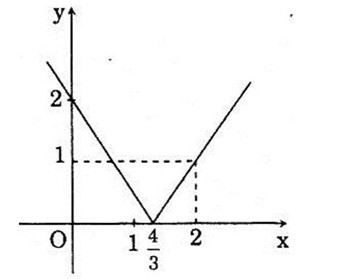
Bảng biến thiên 

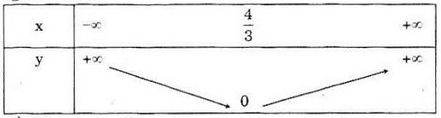
b) Đồ thị hàm số 

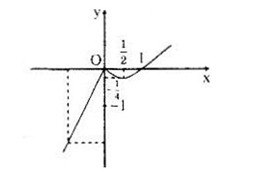
Bảng biến thiên

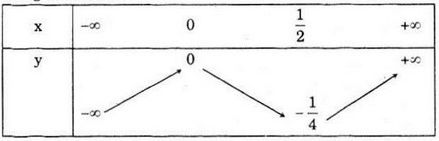
c) Ta có 

\(y = \left\{ {\begin{array}{*{20}{l}}
{\frac{1}{2}{x^2} + x - \frac{3}{2},{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} x \le  - 3,x \ge  - 1}\\
{ - \frac{1}{2}{x^2} - x + \frac{3}{2},{\mkern 1mu} {\mkern 1mu}  - 3 < x < 1}
\end{array}} \right.\)

Đồ thị hàm số 

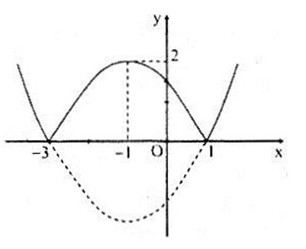
Bảng biến thiên

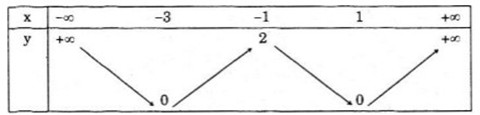
d) Ta có 

\(y = \left\{ {\begin{array}{*{20}{l}}
{{x^2} - 2x - 1,\,\,x \ge 0}\\
{ - {{\left( {x + 1} \right)}^2},\,\,x < 0}
\end{array}} \right.\)

Đồ thị hàm số 

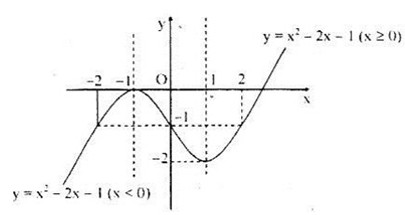
Bảng biến thiên 

-- Mod Toán 10 HỌC247