Giải bài 10 tr 51 sách GK Toán ĐS lớp 10
Lập bảng biến thiên và vẽ đồ thị của các hàm số
a) \(y = {x^2} - 2x - 1;\)
b) \(y = - {x^2} + 3x + 2\)
Hướng dẫn giải chi tiết bài 10
Câu a:
Hàm số \(y = {x^2} - 2x - 1\) có tập xác định là \(\mathbb{R}\)
Chiều biến thiên:
Vì hàm số \(y = {x^2} - 2x - 1\) có hệ số a = 1 > 0 nên ta có:
Hàm số đồng biến trên khoảng \((1; + \infty )\) và nghịch biến trên khoảng \(( - \infty ; - 1)\)
Bảng biến thiên:

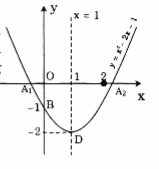
Đồ thị: Đồ thị của hàm số \(y = {x^2} - 2x - 1\) là một parabol có toạ độ đỉnh là D(1; -2) có trục đối xứng là đường thẳng x = 1
Giao của đồ thị với trục Oy là B(0; -1)
Đồ thị giao với Ox tại hai điểm: \({A_1}(1 - \sqrt 2 ;0);\,\,{A_2}(1 + \sqrt 2 ;0)\)
Đồ thị là hình vẽ bên:
Câu b:
Hàm số \(y = - {x^2} + 3x + 2\) có tập xác định là tập \(\mathbb{R}\)
Chiều biến thiên: Hàm số \(y = - {x^2} + 3x + 2\)có hệ số a = -1< 0 nên ta có: Hàm số đồng biến trên khoảng \(( - \infty ;\frac{3}{2})\) và nghịch biến trên khoảng \((\frac{3}{2}; + \infty )\)
Bảng biến thiên: Khi x dần tới \( - \infty \) thì y dần tới \( - \infty \), khi x dần tới \( + \infty \) thì y dần tới \( - \infty \), khi \(x = \frac{3}{2}\) ta có \(y = \frac{{17}}{4}\), ta có bảng biến thiên
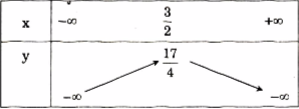
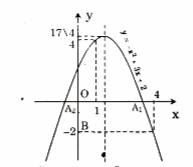
Đồ thị: Đồ thị hàm số \(y = - {x^2} + 3x + 2\)là một parabol, toạ độ đỉnh là \(D = (\frac{3}{2};\frac{{17}}{4})\) trục đối xứng là đường thẳng \(x = \frac{3}{2}\).
Đồ thị giao với Oy tại điểm B(0;2)
Đồ thị giao với Ox tại hai điểm:
\({A_1} = \left( {\frac{{3 + \sqrt {17} }}{2};0} \right);{A_2} = \left( {\frac{{3 - \sqrt {17} }}{2};0} \right)\)
-- Mod Toán 10 HỌC247
-


A. \(y = 4{x^2} - 3x + 1\) .
B. \(y = - {x^2} + \frac{3}{2}x + 1\) .
C. \(y = - 2{x^2} + 3x + 1\) .
D. \(y = {x^2} - \frac{3}{2}x + 1\) .
Theo dõi (0) 1 Trả lời -


A. - 1. B. 1.
C. 5. D. - 5.
Theo dõi (0) 1 Trả lời -


Tìm tập xác định của hàm số \(y = \sqrt {{x^2} - 2x - 15} + \sqrt {6 - x} \)
bởi Trịnh Lan Trinh
 30/05/2020
Theo dõi (0) 1 Trả lời
30/05/2020
Theo dõi (0) 1 Trả lời -


Cho hàm số \(f\left( x \right) = \sqrt {x - 1} + \frac{1}{{x - 3}}\). Tập nào sau đây là tập xác định của hàm số f(x)?
bởi Nguyễn Lệ Diễm
 30/05/2020
30/05/2020
A. \(\left( {1; + \infty } \right)\).
B. \(\left[ {1; + \infty } \right)\).
C. \(\left[ {1;3} \right) \cup \left( {3; + \infty } \right)\).
D. \(\left( {1; + \infty } \right)\backslash \left\{ 3 \right\}\).
Theo dõi (0) 1 Trả lời -


Tìm tập xác định của hàm số \(y = \frac{{x + 3}}{{\sqrt {{x^2} + 6x + 9} }}\)
bởi Trịnh Lan Trinh
 31/05/2020
Theo dõi (0) 1 Trả lời
31/05/2020
Theo dõi (0) 1 Trả lời -


Tìm tập xác định của hàm số \(y = f\left( x \right) = \frac{{\sqrt {x - 1} }}{{{x^2} - 4}}\)
bởi Nguyễn Lệ Diễm
 31/05/2020
Theo dõi (0) 1 Trả lời
31/05/2020
Theo dõi (0) 1 Trả lời -


Cho hàm số \(y = \left\{ \begin{array}{l} \frac{2}{{x - 1}},x \in \left( { - \infty ;0} \right)\\ \sqrt {x + 1} ,x \in \left[ {0;2} \right]\\ {x^2} - 1,x \in \left( {2;5} \right] \end{array} \right.\). Tính f(4), ta được kết quả:
bởi Trần Bảo Việt
 31/05/2020
Theo dõi (0) 1 Trả lời
31/05/2020
Theo dõi (0) 1 Trả lời -


Tìm m để đường thẳng y= m cắt đồ thị hàm số y = x | x − 2 | tại điểm một điểm duy nhất.
bởi Trần Bảo Việt
 30/05/2020
Theo dõi (0) 1 Trả lời
30/05/2020
Theo dõi (0) 1 Trả lời -


Parabol (P) y= m^2x^2 và đường thẳng (d) y= -4x-1 cắt nhau tại hai điểm phân biệt ứng với:
bởi Nguyễn Lệ Diễm
 30/05/2020
30/05/2020
A. Mọi giá trị m.
B. Mọi m≠ 2.
C. Mọi m thỏa mãn |m|<2 và m≠0
D. Mọi m< 4 và m≠0.
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 8 trang 50 SGK Đại số 10
Bài tập 9 trang 50 SGK Đại số 10
Bài tập 11 trang 51 SGK Đại số 10
Bài tập 12 trang 51 SGK Đại số 10
Bài tập 2.27 trang 42 SBT Toán 10
Bài tập 2.28 trang 42 SBT Toán 10
Bài tập 2.29 trang 43 SBT Toán 10
Bài tập 2.30 trang 43 SBT Toán 10
Bài tập 2.31 trang 43 SBT Toán 10
Bài tập 2.32 trang 43 SBT Toán 10
Bài tập 2.33 trang 43 SBT Toán 10
Bài tập 39 trang 63 SGK Toán 10 NC
Bài tập 40 trang 63 SGK Toán 10 NC
Bài tập 41 trang 63 SGK Toán 10 NC
Bài tập 42 trang 63 SGK Toán 10 NC
Bài tập 43 trang 63 SGK Toán 10 NC
Bài tập 44 trang 64 SGK Toán 10 NC





