Bài tập 43 trang 63 SGK Toán 10 NC
Xác định các hệ số a, b và c để cho hàm số \(y=ax^2+bx+c\) đạt giá trị nhỏ nhất bằng \(\frac{3}{4}\) khi \(x = \frac{1}{2}\) và nhận giá trị bằng 1 khi x = 1. Lập bảng biến thiên và vẽ đồ thị của hàm số.
Hướng dẫn giải chi tiết
Đặt \(f(x)=ax^2+bx+c\)
Ta có
\(\left\{ \begin{array}{l}
{x_1} = - \frac{b}{{2a}}\\
f\left( {\frac{1}{2}} \right) = \frac{1}{4}a + \frac{1}{2}b + c\\
f\left( 1 \right) = a + b + c
\end{array} \right.\)
Tìm hệ số \(a, b, c\) thỏa hệ:
\(\begin{array}{l}
\left\{ {\begin{array}{*{20}{l}}
{ - \frac{b}{{2a}} = \frac{1}{2}}\\
{\frac{1}{4}a + \frac{1}{2}b + c = \frac{3}{4}}\\
{a + b + c = 1}
\end{array}} \right.\\
\Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{a + b = 0}\\
{a + 2b + 4 = 3}\\
{a + b + c = 1}
\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{a = 1}\\
{b = - 1}\\
{c = 1}
\end{array}} \right.
\end{array}\)
Vậy \(y=x^2-x+1\)
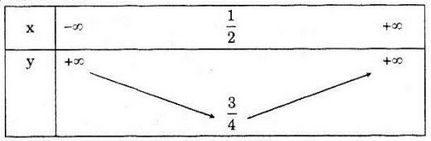
Bảng biến thiên
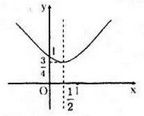
Đồ thị hàm số
-- Mod Toán 10 HỌC247
-


Tìm GTNN của hàm số y=(2x^2-x+2)/(2x-1)
bởi Lê Bảo An
 06/11/2018
06/11/2018
tìm g/trị nhỏ nhất của hàm số:
y=\(\dfrac{2x^2-x+2}{2x-1}\)vs ∀ x∈(\(\dfrac{1}{2}\);+∞)
Theo dõi (0) 1 Trả lời -


Tìm a, b, c biết 1/2a=2/3b=3/4c và a-b=15
bởi Trịnh Lan Trinh
 06/11/2018
06/11/2018
hj các man giúp heo câu này na
tìm a,b,c biết \(\dfrac{1}{2}a=\dfrac{2}{3}b=\dfrac{3}{4}c\)và a-b =15
Theo dõi (0) 1 Trả lời -


Tính P(3) biết P(x)=ax^3+bx^2+cx+d, P(0)=1 và P(2)=120
bởi thu trang
 24/09/2018
24/09/2018
Cho đa thức P(x)=ax^3+bx^2+cx+d(a # 0). Biết P91)=100;P(-1)=50;P(0)=1;P(2)=120 . Tính P(3)
 khó quá......>.<Theo dõi (0) 1 Trả lời
khó quá......>.<Theo dõi (0) 1 Trả lời -


Bài 24 trang 42 sách bài tập Đại số 10
bởi Tran Chau
 06/11/2018
Bài 24 (SBT trang 42)
06/11/2018
Bài 24 (SBT trang 42)Vẽ đồ thị của hàm số :
\(y=\left|\dfrac{2}{3}x^2-\dfrac{8}{3}x+2\right|\)
Theo dõi (0) 1 Trả lời -


Tìm x để hàm số y=x^2-2x-1 bé hơn 0, lớn hơn 0
bởi Ngoc Nga
 12/10/2018
12/10/2018
Cho hàm số y=x2-2x-1 (P) , y=2x+1 (Δm)
a/ Tìm x để y>0, y<0, yminb/ Tìm giao điểm của (P) và đường thẳng :(Δ1): y=2x+1Theo dõi (0) 1 Trả lời -


xét tính đồng biến nghịch biến của hàm số
a)\(y=f\left(x\right)=\sqrt{x^2+2x+3}\)
b) \(y=f\left(x\right)=x-\sqrt{1-x}\) với x<1
Theo dõi (0) 1 Trả lời -


Xác định hàm số f(x), biết f(x+1)=x^2-3x+2
bởi Nguyễn Ngọc Sơn
 24/09/2018
24/09/2018
Xác định hàm số f(x) biết f(x+1)=x^2-3x+2
Theo dõi (0) 1 Trả lời -


Tìm các số nguyên dương x, y, z thỏa x+y+z > 11
bởi Dương Quá
 24/09/2018
24/09/2018
Tìm tất cả các số nguyên dương x, y, z thỏa mãn: x+y+z>11 và 8x+9y+10z=100
các bn hok giỏi giúp mik nha
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


TIm a,b,c và định a để hàm số xác định trên (0;1)
bởi Hà Nhân
 11/11/2017
11/11/2017
Bài 1: Cho Parapol (p) \(y=ax^2+bx+c\) đạt gái trị nhỏ nhất bằng -25 khi x=1 và cắt trụ hoành tại điểm có hoàng độ bằng -4 thì a,b,c có giá trị nào ???
Bài 2: Định a để hàm số \(y=\frac{1}{\sqrt{x-a}}+\sqrt{-x+2a+6}\) xác định trên (0;1)Theo dõi (0) 3 Trả lời





