Bài tập 42 trang 63 SGK Toán 10 NC

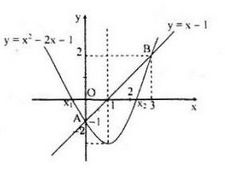
a) Đường thẳng \(d: y=x-1\) qua A(0;- 1); B(1;0)

Parabol (P): \(y=x^2-2x-1\) có đỉnh S(1;- 2)

Phương trình hoành độ giao điểm của d và (P) là:

\(\begin{array}{l}
{x^2} - 2x - 1 = x - 1\\
 \Leftrightarrow {x^2} - 3x = 0\\
 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = 0\left( {y =  - 1} \right)}\\
{x = 3\left( {y = 2} \right)}
\end{array}} \right.
\end{array}\)

Giao điểm của d và (P) là A(0;- 1) và C(3;2)

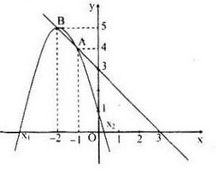
b) Đường thẳng \(d: y=-x+3\) qua A(0;3); B(3;0)

Parabol (P): \(y=-x^2-4x+1\) có đỉnh S(- 2;5)

Phương trình hoành độ giao điểm của d và (P) là:

\(\begin{array}{*{20}{l}}
{ - {x^2} - 4x + 1 =  - x + 3}\\
\begin{array}{l}
 \Leftrightarrow {x^2} + 3x + 2 = 0\\
 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x =  - 1\left( {y = 4} \right)}\\
{x =  - 2\left( {y = 5} \right)}
\end{array}} \right.
\end{array}
\end{array}\)

Giao điểm của d và (P) là (- 1;4) và (- 2;5)

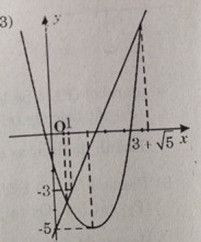
c) Đường thẳng \(d: y=2x-5\) đi qua A(0;- 5); B(1;- 3)

Parabol (P): \(y=x^2-4x-1\) có điểnh S(2;- 5)

Phương trình hoành độ giao điểm của d và (P) là:

\(\begin{array}{*{20}{l}}
{{x^2} - 4x - 1 = 2x - 5}\\
\begin{array}{l}
 \Leftrightarrow {x^2} - 6x + 4 = 0\\
 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = 3 - \sqrt 5 \left( {y = 1 - 2\sqrt 5 } \right)}\\
{x = 3 + \sqrt 5 \left( {y = 1 + 2\sqrt 5 } \right)}
\end{array}} \right.
\end{array}
\end{array}\)

Giao điểm của d và (P) là 

\(\left( {3 - \sqrt 5 ;1 - 2\sqrt 5 } \right);\left( {3 + \sqrt 5 ;1 + 2\sqrt 5 } \right)\)

-- Mod Toán 10 HỌC247