Bài tập 2.29 trang 43 SBT Toán 10

Tập xác định của hàm số là D = R.

f(−x) = (−x)²−2|−x|+1 = x²−2|x|+1 = f(x)

Hàm số là hàm số chẵn. Đồ thị của nó nhận trục tung làm trục đối xứng.

Để xét chiều biến thiên và vẽ đồ thị của nó chỉ cần xét chiều biến thiên và vẽ đồ thị của nó trên nửa khoảng [0;+∞), rồi lấy đối xứng qua Oy.

Với x ≥ 0 có f(x) = x²−2x+1.

Bảng biến thiên

Đồ thị của hàm số đã cho được vẽ ở hình dưới đây.

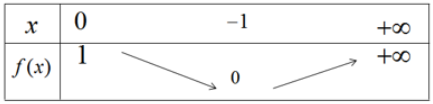
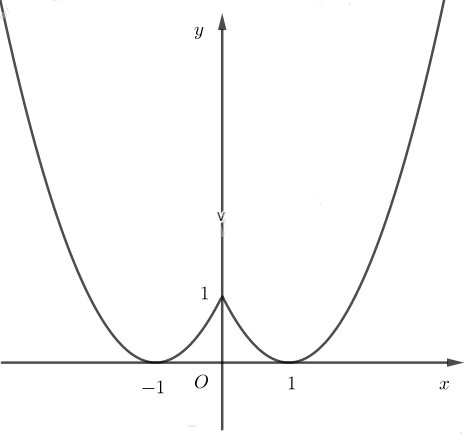
-- Mod Toán 10 HỌC247