Giải bài 2.30 tr 43 SBT Đại số 10
Vẽ đồ thị của hàm số \(y = \left| {\frac{2}{3}{x^2} - \frac{8}{3}x + 2} \right|\)
Hướng dẫn giải chi tiết
Vì \(\left| {f\left( x \right)} \right| = \left\{ \begin{array}{l}
f\left( x \right),f\left( x \right) \ge 0\\
- f\left( x \right),f\left( x \right) < 0
\end{array} \right.\)
Nên để vẽ đồ thị của hàm số y = |f(x)| ta vẽ đồ thị của hàm số y = f(x), sau đó giữ nguyên phần đồ thị ở phía trên trục hoành và lấy đối xứng phần đồ thị nằm phía dưới trục hoành qua trục hoành.
Trong trường hợp này, ta vẽ đồ thị của hàm số \(y = \frac{2}{3}{x^2} - \frac{8}{3}x + 2\), sau đó giữ nguyên phần đồ thị ứng với các nửa khoảng (−∞;1] và [3;+∞).
Lấy đối xứng phần đồ thị ứng với khoảng (1;3) qua trục hoành.
Đồ thị của hàm số \(y = \left| {\frac{2}{3}{x^2} - \frac{8}{3}x + 2} \right|\) được vẽ trên hình sau (đường nét liền)
.jpg)
-- Mod Toán 10 HỌC247
-


Tìm tập xác định của hàm số f(x)=(x+1)/(x-5)
bởi Ốc Ciu
 24/03/2020
24/03/2020
 Theo dõi (0) 4 Trả lời
Theo dõi (0) 4 Trả lời -


Cho tam giác ABC đều cạnh a. Xác định vị trí điểm I thỏa mãn 4*(vectơ IA)+(vectơ IB)+(vectơ IC)=(vectơ 0) vsf tính độ dài IA, IB, IC.
bởi Quỳnh Hoàng
 20/03/2020
20/03/2020
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tìm tham số m để phương trình x^4 2(m-2)x^2 m^2 - 2m = 0 có bốn nghiệm phân biệt
bởi Nguyễn Ngọc Quỳnh Như
 16/03/2020
16/03/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Giải phương trình 1/3y^2-3/5y-11/5=0
bởi Trần Giang
 20/02/2020
20/02/2020
 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tìm 1 vecto cùng phương với vecto a
bởi Diêu Thuy
 13/02/2020
13/02/2020
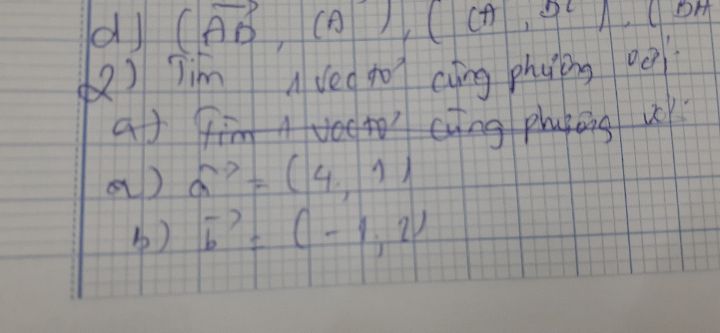 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Lập ptts và pttq của đường thẳng d đi qua A(2;3) và có vecto pháp tuyến n=(7;3)
bởi Ha Vy
 10/02/2020
Bạn nào biết thì giúp mình với ạ huhu bài 1,2,3 mình cũng không rõ nó ở bài nào @@
10/02/2020
Bạn nào biết thì giúp mình với ạ huhu bài 1,2,3 mình cũng không rõ nó ở bài nào @@ Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tìm m để f(x)=(m-3)x^2+2mx-1 > 0 với mọi x thuộc R
bởi Châu Anh
 05/02/2020
05/02/2020
 Theo dõi (1) 2 Trả lời
Theo dõi (1) 2 Trả lời
Bài tập SGK khác
Bài tập 2.28 trang 42 SBT Toán 10
Bài tập 2.29 trang 43 SBT Toán 10
Bài tập 2.31 trang 43 SBT Toán 10
Bài tập 2.32 trang 43 SBT Toán 10
Bài tập 2.33 trang 43 SBT Toán 10
Bài tập 39 trang 63 SGK Toán 10 NC
Bài tập 40 trang 63 SGK Toán 10 NC
Bài tập 41 trang 63 SGK Toán 10 NC
Bài tập 42 trang 63 SGK Toán 10 NC
Bài tập 43 trang 63 SGK Toán 10 NC
Bài tập 44 trang 64 SGK Toán 10 NC





