Giải bài 3.19 tr 155 SBT Hình học 10
Lập phương trình của đường tròn (C) đi qua hai điểm A(1; 2), B(3; 4) và tiếp xúc với đường thẳng Δ: 3x + y - 3 = 0
Hướng dẫn giải chi tiết
\(\begin{array}{l}
\left\{ \begin{array}{l}
I{A^2} = I{B^2}\\
{\left[ {d\left( {I,\Delta } \right)} \right]^2} = I{A^2}
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
{\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} = {\left( {x - 3} \right)^2} + {\left( {y - 4} \right)^2}\\
\frac{{{{\left( {3x + y - 3} \right)}^2}}}{{10}} = {\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2}
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
- 2x - 4y + 5 = - 6x - 8y + 25\\
9{x^2} + {y^2} + 9 + 6xy - 6y - 18x = 10{x^2} - 20x + 10 + 10{y^2} - 40y + 40
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
x + y - 5 = 0\\
{x^2} + 9{y^2} - 6xy - 2x - 34y + 41 = 0
\end{array} \right.
\end{array}\)
Giải hệ phương trình ta được \(\left[ \begin{array}{l}
\left\{ \begin{array}{l}
x = 4\\
y = 1
\end{array} \right.\\
\left\{ \begin{array}{l}
x = \frac{3}{2}\\
y = \frac{7}{2}
\end{array} \right.
\end{array} \right.\)
Vậy \(\left[ \begin{array}{l}
\left( {{C_1}} \right):{x^2} + {y^2} - 8x - 2y + 7 = 0\\
\left( {{C_2}} \right):{x^2} + {y^2} - 3x - 7y + 12 = 0
\end{array} \right.\)
-- Mod Toán 10 HỌC247
-


Cho trước ba đường thẳng d1,d2,d3 phân biệt. Gọi m là số đường tròn có tâm nằm trên d1 và cùng tiếp xúc với d2,d3. Khẳng định nào sau đây không thể xảy ra?
bởi hà trang
 21/01/2021
21/01/2021
A. m = 0
B. m = 1
C. m = 2
D. m = 3
Theo dõi (0) 1 Trả lời -


Cho đường tròn (C) có tâm I(-4;2) và bán kính R = 5. Khi đó phương trình của (C) là:
bởi Sam sung
 21/01/2021
21/01/2021
A. x2+y2-4x+2y-5=0
B. x2+y2+8x-4y-5=0
C. x2+y2-8x+4y-5=0
D. x2+y2+8x-4y-25=0
Theo dõi (0) 1 Trả lời -


Cho đường tròn (C) có phương trình \({x^2} + {y^2} + 4x - 6y - 3 = 0\). Khi đó đường tròn có tâm I và bán kính R với
bởi thu hảo
 22/01/2021
22/01/2021
A. I(4; -6), R = 4
B. I(-2; 3), R = 16
C. I(-4; 6), R = 4
D. I(-2; 3), R = 4
Theo dõi (0) 1 Trả lời -


Cho đường tròn (C) có phương trình \({\left( {x - 2} \right)^2} + {\left( {y + 1} \right)^2} = 4\). Khi đó đường tròn có tâm I và bán kính R với
bởi Minh Thắng
 22/01/2021
22/01/2021
A. I(-2; 1), R = 4
B. I(2; -1), R = 4
C. I(2; -1), R = 2
D. I(-2; 1), R = 2
Theo dõi (0) 1 Trả lời -


Viết phương trình đường tròn C có đường kính AB(-1;2) và đi qua điểm M(2;1)?
bởi Lê Trần Xuân Huy
 29/06/2020
29/06/2020
Câu 3. Cho 2 điểm A (5;-1), B(-3;7). Viết phương trình đường tròn C có đường kính AB(-1;2) và đi qua điểm M(2;1)?
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Viết phương trình đường tròn đường kính PQ?
bởi Thu Huỳnh
 25/06/2020
Trong mặt phẳng Oxy, cho hai điểm P(-1;4), Q(-5;4). Đường tròn đường kính PQ có phương trình làTheo dõi (1) 0 Trả lời
25/06/2020
Trong mặt phẳng Oxy, cho hai điểm P(-1;4), Q(-5;4). Đường tròn đường kính PQ có phương trình làTheo dõi (1) 0 Trả lời -


Bài 38
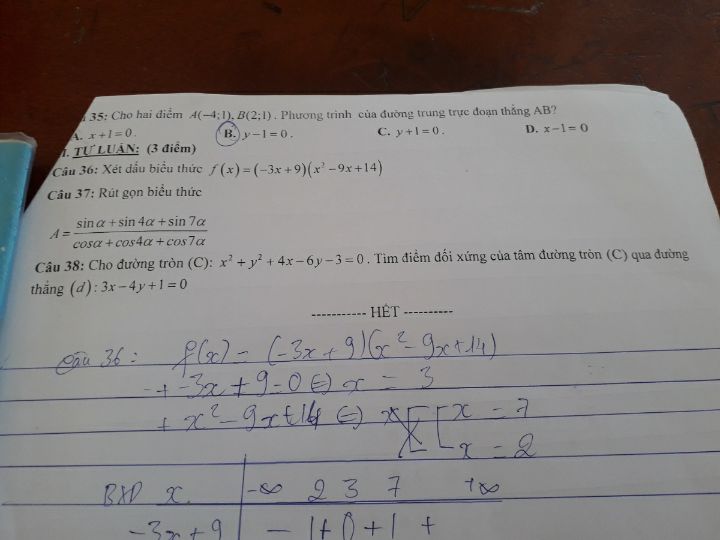 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 3.17 trang 155 SBT Hình học 10
Bài tập 3.18 trang 155 SBT Hình học 10
Bài tập 3.20 trang 155 SBT Hình học 10
Bài tập 3.21 trang 155 SBT Hình học 10
Bài tập 3.22 trang 155 SBT Hình học 10
Bài tập 3.23 trang 155 SBT Hình học 10
Bài tập 3.24 trang 156 SBT Hình học 10
Bài tập 3.25 trang 156 SBT Hình học 10
Bài tập 3.26 trang 156 SBT Hình học 10
Bài tập 3.27 trang 156 SBT Hình học 10
Bài tập 21 trang 95 SGK Hình học 10 NC
Bài tập 22 trang 95 SGK Hình học 10 NC
Bài tập 23 trang 95 SGK Hình học 10 NC
Bài tập 24 trang 95 SGK Hình học 10 NC
Bài tập 25 trang 95 SGK Hình học 10 NC
Bài tập 26 trang 95 SGK Hình học 10 NC
Bài tập 27 trang 96 SGK Hình học 10 NC





