Giải bài 3.24 tr 156 SBT Hình học 10
Lập phương trình tiếp tuyến Δ của đường tròn (C): x2 + y2 - 6x + 2y = 0 biết rằng Δ vuông góc với đường thẳng d: 3x - y + 4 = 0
Hướng dẫn giải chi tiết
Δ vuông góc với d nên phương trình Δ có dạng: x + 3y + c = 0
(C) có tâm I(3;-1) và có bán kính R = \(\sqrt {10} \). Ta có:
Δ tiếp xúc với (C) :
\( \Leftrightarrow d\left( {I,\Delta } \right) = R \Leftrightarrow \frac{{\left| {3 - 3 + c} \right|}}{{\sqrt {10} }} = \sqrt {10} \Leftrightarrow c = \pm 10\)
Vậy có hai tiếp tuyến thỏa mãn đề bài là:
Δ1: x + 3y + 10 = 0 và Δ2: x + 3y - 10 = 0
-- Mod Toán 10 HỌC247
-


Viết phương trình đường tròn có tâm I thuộc đường thẳng d : x+2y-2=0, bán kính R=5, tiếp xúc với đường thẳng d':3x-4y-11=0
bởi H. Như
 20/04/2020
20/04/2020
Viêt phương rrinhf đường tròn có tâm I thuộc đương thẳng d : x+2y-2=0 ,bán kính R=5, tiếp xúc với đường thẳng d':3x-4y-11=0
Theo dõi (0) 1 Trả lời -


Tìm tâm và bán kính đường tròn (x-3)^2+(y-6)^2=16
bởi Phan Kim Ngân
 17/04/2020
17/04/2020
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Viết phương trình tiếp tuyến của (c) tạo với hai trục tọa độ một tam giác vuông cân
bởi Nguyễn Mai Ly
 12/04/2020
12/04/2020
Cho (c): (x-2)^2 y^2=4. Viết phương trình tiếp tuyến của (c) tạo với hai trục tọa độ một tam giác vuông cân
Theo dõi (0) 0 Trả lời -


Cho tan a - 4 cot a =0 và pi < a < 3pi/2. Tính giá trị của A= sin a + cos a.
bởi Huy Nguyễn
 02/04/2020
02/04/2020
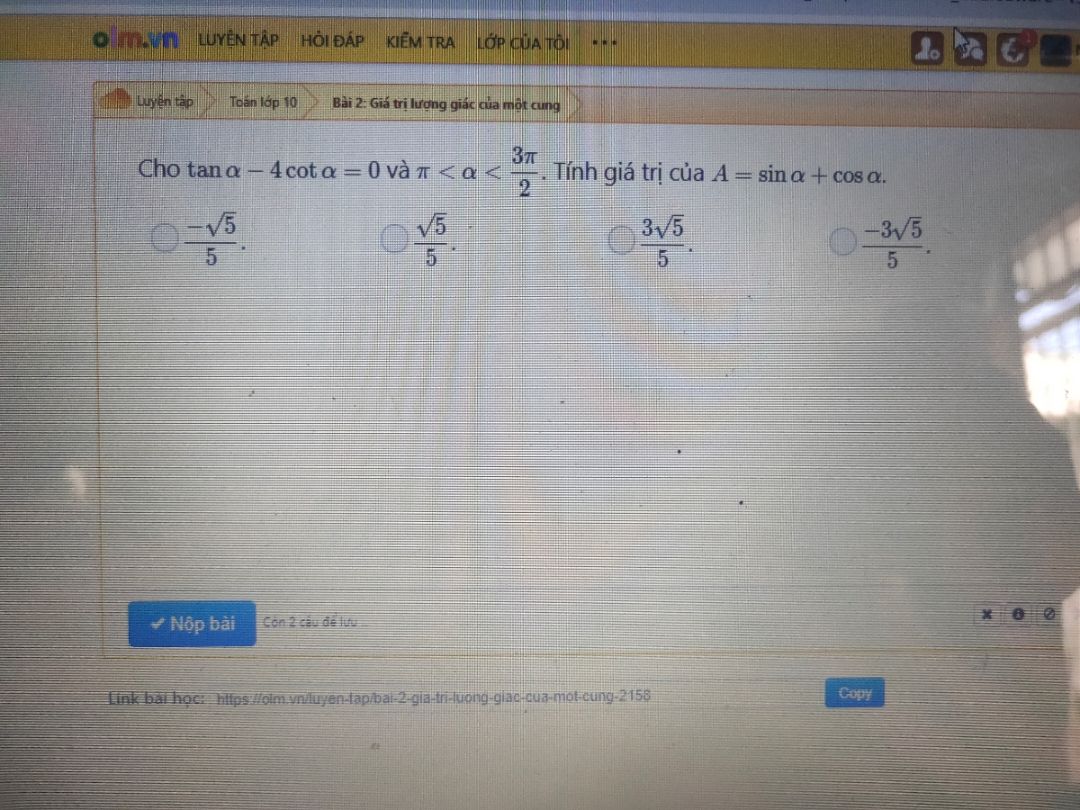 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Trong mặt phẳng tọa độ Oxy, cho hình thoi ABCD có B(1,2) và tam giác ABC nội tiếp đường tròn đường kính AK. Biết BC có phương trình 2x y-4=0, điểm K thuộc đường thẳng d:4x-2y-15=0 và đường thẳng CD đi qua M(4;7/2). Tính tích các hoành độ đỉnh A,C,D
bởi Nguyễn Hương Giang
 31/03/2020
Trong mặt phẳng tọa độ Oxy, cho hình thoi ABCD có B(1,2) và tam giác ABC nội tiếp đường tròn đường kính AK. Biết BC có phương trình 2x y-4=0, điểm K thuộc đường thẳng d:4x-2y-15=0 và đường thẳng CD đi qua M(4;7/2). Tính tích các hoành độ đỉnh A,C,DTheo dõi (0) 3 Trả lời
31/03/2020
Trong mặt phẳng tọa độ Oxy, cho hình thoi ABCD có B(1,2) và tam giác ABC nội tiếp đường tròn đường kính AK. Biết BC có phương trình 2x y-4=0, điểm K thuộc đường thẳng d:4x-2y-15=0 và đường thẳng CD đi qua M(4;7/2). Tính tích các hoành độ đỉnh A,C,DTheo dõi (0) 3 Trả lời -


Viết phương trình đường tròn có đường kính AB, với: A(−2;3), B(6;5) 2) A(−3;4), B(7;2)
bởi Le Ngan
 29/03/2020
Viết phương trình đường tròn có đường kính AB, với: 1) A(−2;3), B(6;5) 2) A(−3;4), B(7;2)Theo dõi (0) 4 Trả lời
29/03/2020
Viết phương trình đường tròn có đường kính AB, với: 1) A(−2;3), B(6;5) 2) A(−3;4), B(7;2)Theo dõi (0) 4 Trả lời
Bài tập SGK khác
Bài tập 3.22 trang 155 SBT Hình học 10
Bài tập 3.23 trang 155 SBT Hình học 10
Bài tập 3.25 trang 156 SBT Hình học 10
Bài tập 3.26 trang 156 SBT Hình học 10
Bài tập 3.27 trang 156 SBT Hình học 10
Bài tập 21 trang 95 SGK Hình học 10 NC
Bài tập 22 trang 95 SGK Hình học 10 NC
Bài tập 23 trang 95 SGK Hình học 10 NC
Bài tập 24 trang 95 SGK Hình học 10 NC
Bài tập 25 trang 95 SGK Hình học 10 NC
Bài tập 26 trang 95 SGK Hình học 10 NC
Bài tập 27 trang 96 SGK Hình học 10 NC





