Phần hướng dẫn giải bài tập Hình học 8 Bài 7 Hình bình hành sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng, giải bài tập từ SGK Hình học 8 Tập 1
-
Bài tập 43 trang 92 SGK Toán 8 Tập 1
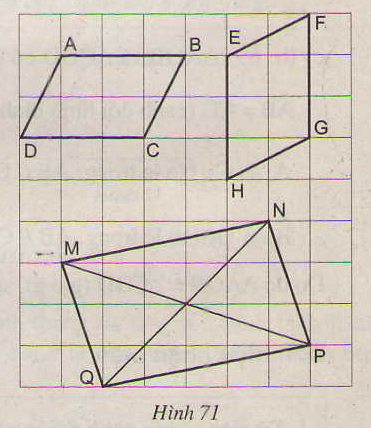
Các tứ giác ABCD, EFGH, MNPQ trên giấy kẻ ô vuông ở hình 71 có là hình bình hành hay không ?
-
Bài tập 44 trang 92 SGK Toán 8 Tập 1
Cho hình bình hành ABCD. Gọi E là trung điểm của AD, F là trung điểm của BC. Chứng minh rằng BE = DF.
-
Bài tập 45 trang 92 SGK Toán 8 Tập 1
Cho hình bình hành ABCD (AB > BC). Tia phân giác của góc D cắt AB ở E, tia phân giác của góc B cắt CD ở F.
a) Chứng minh rằng DE // BF.
b) Tứ giác DEBF là hình gì? Vì sao ?
-
Bài tập 46 trang 92 SGK Toán 8 Tập 1
Các câu sau đúng hay sai ?
a) Hình thang có hai cạnh đáy bằng nhau là hình bình hành.b) Hình thang có hai cạnh bên song song là hình bình hành.
c) Tứ giác có hai cạnh đối bằng nhau là hình bình hành.
d) Hình thang có hai cạnh bên bằng nhau là hình bình hành.
-
Bài tập 47 trang 93 SGK Toán 8 Tập 1
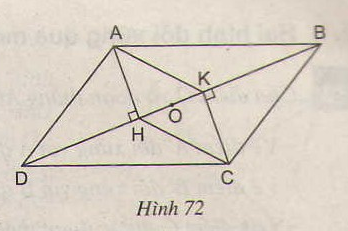
Cho hình 72, trong đó ABCD là hình bình hành.
a) Chứng minh rằng AHCK là hình bình hành.
b) Gọi O là trung điểm của HK. Chứng minh rằng ba điểm A, O, C thẳng hàng
-
Bài tập 48 trang 93 SGK Toán 8 Tập 1
Tứ giác ABCD có E, F, G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì ? Vì sao ?
-
Bài tập 49 trang 93 SGK Toán 8 Tập 1
Cho hình bình hành ABCD. Gọi I, K theo thứ tự là trung điểm của CD, AB. Đường chéo BD cắt AI, CK theo thứ tự ở M và N. Chứng minh rằng:
a) AI // CK
b) DM = MN = NB
-
Bài tập 73 trang 89 SBT Toán 8 Tập 1
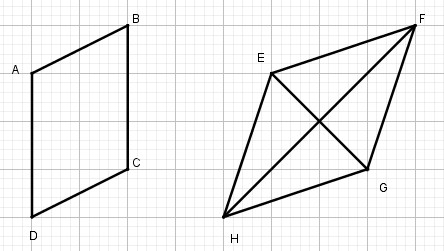
Các tứ giác ABCD, EFGH vẽ trên giấy kẻ ô vuông ở hình 7 có là hình bình hành không ?
-
Bài tập 74 trang 89 SBT Toán 8 Tập 1
Cho hình bình hành ABCD. Gọi E là trung điểm của AB, F là trung điểm của CD. Chứng minh rằng DE = BF.
-
Bài tập 75 trang 89 SBT Toán 8 Tập 1
Cho hình bình hành ABCD. Tia phân giác của góc A cắt CD ở M. Tia phân giác của góc C cắt AB ở N. Chứng minh rằng AMCN là hình bình hành.
-
Bài tập 76 trang 89 SBT Toán 8 Tập 1
Trên hình 8, cho ABCD là hình bình hành. Chứng minh rằng AECF là hình bình hành.
-
Bài tập 77 trang 89 SBT Toán 8 Tập 1
Tứ giác ABCD có E, F, G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì ? Vì sao ?
-
Bài tập 78 trang 89 SBT Toán 8 Tập 1
Cho hình bình hành ABCD. Gọi I, K theo thứ tự là trung điểm của CD , AB. Đường chéo BD cắt AI, CK theo thứ tự ở E, F. Chứng minh rằng DE = EF = FB.
-
Bài tập 79 trang 89 SBT Toán 8 Tập 1
Tính các góc của hình bình hành ABCD, biết:
a. \(\widehat A = {110^0}\)
b. \(\widehat A - \widehat B = {20^0}\)
-
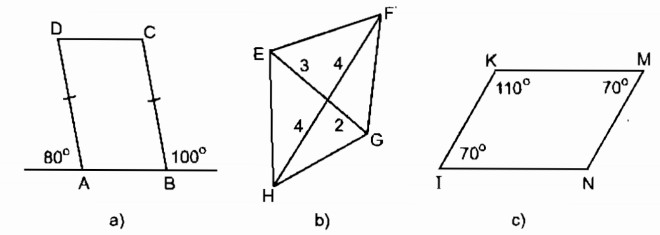
Bài tập 80 trang 89 SBT Toán 8 Tập 1
Trong các tứ giác trên hình 9, tứ giác nào là hình bình hành ?
-
Bài tập 81 trang 90 SBT Toán 8 Tập 1
Chu vi hình bình hành \(ABCD\) bằng \(10cm,\) chu vi tam giác \(ABD\) bằng \(9cm.\) Tính độ dài \(BD.\)
-
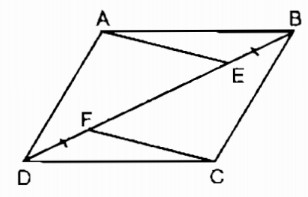
Bài tập 82 trang 90 SBT Toán 8 Tập 1
Trên hình 10, cho ABCD là hình bình hành. Chứng minh rằng AE // CF.
-
Bài tập 83 trang 90 SBT Toán 8 Tập 1
Cho hình bình hành \(ABCD.\) Gọi \(E,\) \(F\) theo thứ tự là trung điểm của \(AB,\) \(CD.\) Gọi \(M\) là giao điểm của \(AF\) và \(DE,\) \(N\) là giao điểm của \(BF\) và \(CE.\) Chứng minh rằng :
\(a)\) \(EMFN\) là hình bình hành.
\(b)\) Các đường thẳng \(AC,\) \(EF,\) \(MN\) đồng quy.
-
Bài tập 84 trang 90 SBT Toán 8 Tập 1
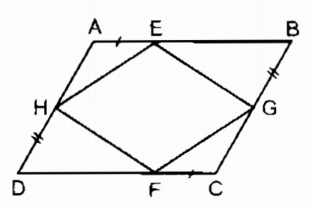
Trên hình 11, cho ABCD là hình bình hành. Chứng minh rằng:
a. EGFH là hình bình hành
b. Các đường thẳng AC, BD, EF, GH đồng quy.
-
Bài tập 85 trang 90 SBT Toán 8 Tập 1
Cho hình bình hành ABCD. Qua C kẻ đường thẳng xy chỉ có một điểm chung C với hình bình hành. Gọi AA’, BB’, DD’ là các đường vuông góc kẻ từ A, B, D đến đường thẳng xy. Chứng ming rằng AA’ = BB’ + DD’.
-
Bài tập 86 trang 90 SBT Toán 8 Tập 1
Cho hình bình hành ABCD và đường thẳng xy không có điểm chung với hình bình hành. Gọi AA’, BB’, CC’, DD’ là đường vuông góc kẻ từ A, B, C, D đến đường thẳng xy. Tìm mối liên hệ độ dài giữa AA’, BB’, CC’, DD’.
-
Bài tập 87 trang 90 SBT Toán 8 Tập 1
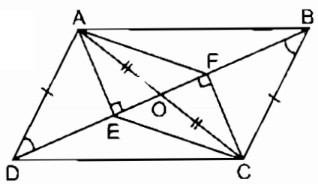
Cho hình bình hành ABCD có \(\widehat A = \alpha > {90^0}\). Ở phía ngoài hình bình hành, vẽ các tam giác đều ADF, ABE.
a. Tính \(\widehat {EAF}\)
b. Chứng minh rằng tam giác CEF là tam giác đều.
-
Bài tập 88 trang 90 SBT Toán 8 Tập 1
Cho tam giác \(ABC.\) Ở phía ngoài tam giác, vẽ các tam giác vuông cân tại \(A\) là \(ABD, ACE.\) Vẽ hình bình hành \(ADIE.\) Chứng minh rằng:
\(a)\) \(IA = BC.\)
\(b)\) \(IA ⊥ BC.\)
-
Bài tập 89 trang 91 SBT Toán 8 Tập 1
Dựng hình bình hành ABCD, biết:
a. AB = 2cm, AD = 3cm, \(\widehat A = {110^0}\)
b. AC = 4cm, BD = 5cm, \(\widehat {BOC} = {50^0}\) (O là giao điểm của hai đường chéo).
-
Bài tập 90 trang 91 SBT Toán 8 Tập 1
Cho ba điểm A, B, C trên giấy kẻ ô vuông (h.12). Hãy vẽ điểm thứ tư M sao cho A, B, C, M là bốn đỉnh của một hình bình hành

-
Bài tập 91 trang 91 SBT Toán 8 Tập 1
Cho tam giác ABC. Dựng đường thẳng song song với BC, cắt cạnh AB ở E, cắt cạnh AC ở F sao cho BE = AF.
-
Bài tập 7.1 trang 91 SBT Toán 8 Tập 1
Tứ giác ABCD là hình bình hành nếu:
A. AB = CD;
B. AD = BC;
C. AB // CD và AD = BC;
D. AB = CD và AD = BC.
-
Bài tập 7.2 trang 91 SBT Toán 8 Tập 1
Cho hình bình hành ABCD , các đường chéo cắt nhau tại O. Gọi E, F theo thứ tự là trung điểm của OD, OB. Gọi K là giao điểm của AE và CD. Chứng minh rằng:
a. AE song song CF
b. DK \( = {1 \over 2}\)KC
-
Bài tập 7.3 trang 91 SBT Toán 8 Tập 1
Cho hình bình hành ABCD. Lấy điểm E trên cạnh AB, điểm F trên cạnh CD sao cho AE = CF. Chứng minh rằng ba đường thẳng AC, BD, EF đồng quy.






