Giải bài 81 tr 90 sách BT Toán lớp 8 Tập 1
Chu vi hình bình hành \(ABCD\) bằng \(10cm,\) chu vi tam giác \(ABD\) bằng \(9cm.\) Tính độ dài \(BD.\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
Sử dụng kiến thức:
+) Trong hình bình hành, các cạnh đối bằng nhau.
+) Chu vi tứ giác bằng tổng 4 cạnh, chu vi tam giác bằng tổng 3 cạnh.
Lời giải chi tiết
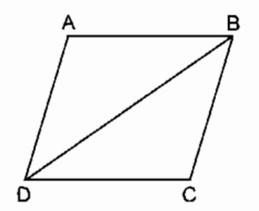
Vì ABCD là hình bình hành nên \(AB=DC, AD=BC\) (tính chất)
Chu vi hình bình hành \(ABCD\) là \(AB+DC+BC+AD\)\(=2AB+2AD=2(AB+AD)\)
Mà chu vi hình bình hành \(ABCD\) bằng \(10cm\) (giả thiết)
Nên \((AB + AD).2 = 10\;\; (cm)\)
\(⇒ AB + AD = \displaystyle {{10} \over 2} =5\) \((cm)\)
Chu vi của \(∆ ABD\) bằng :
\(AB + AD +BD = 9 \;\;(cm)\)
\(⇒ BD = 9 – ( AB + AD)\)\( = 9 – 5 = 4 \;\;(cm)\)
-- Mod Toán 8 HỌC247
-
Chứng minh ba đường thẳng AI,PK,CH đồng qui biết tam giác ABC có E,D,F,H lần lượt là trung điểm AB,AC,BC
bởi Lê Trung Phuong
31/05/2019
Cho tam giác ABC có E,D,F,H lần lượt là trung điểm AB,AC,BC , P nằm trong tam giác ABC . H,I,K lần lượt dối xứng với E,D,F. C/M
a) ACIH là HBH
b) AI,PK,CH đồng qui
Theo dõi (0) 1 Trả lời -
Chứng minh tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành
bởi Trieu Tien
31/05/2019
chứng minh tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành
Theo dõi (0) 1 Trả lời -
Chứng minh tứ giác EKFH là hình bình hành biết O là giao điểm 2 đường chéo AC và BD
bởi Lê Thánh Tông
31/05/2019
Cho hình bình hành ABCD. Gọi O là giao điểm 2 đường chéo AC và BD. Qua O vẽ đường thẳng a cắt AD, BC lần lượt tại E, F. qua O vẽ đường thẳng b cắt AB và CD lần lượt tại K, H. C/m tứ giác EKFH là hình bình hành
Theo dõi (0) 1 Trả lời -
Chứng minh MNEF là hình bình hành biết tam giác ABC có 2 trung tuyến BM, CN cắt nhau tại G
bởi Hong Van
31/05/2019
Cho tam giác ABC, hai trung tuyến BM, CN cắt nhau tại G, gọi E, F lần lượt là trung điểm của GB và GC
a) Chứng minh MNEF là hình bình hành.
b) Lấy I, J thuộc tia đối của MG và NG sao cho MI= MG, NI= NG. Chứng minh BCIJ là hình bình hành.
Theo dõi (0) 1 Trả lời -
Chứng minh NOPQ là hình bình hành biết N, O, P, Q tương ướng là trung điểm AB, BC, CD, DA
bởi sap sua
31/05/2019
Cho tam giác ABCD. Gọi N, O, P, Q tương ướng là trung điểm AB, BC, CD, DA:
a)Chứng minh rằng NOPQ là hình bình hành.b)Nếu có thêm AC vuông góc với BD, chứng minhNOPQ là hình chữ nhật.
Theo dõi (0) 1 Trả lời -
Chứng minh AECF là hình bình hành biết E,F thứ tự là các điểm thuộc BD sao cho BE=EF=FD
bởi Nguyễn Bảo Trâm
31/05/2019
Cho hình bình hành ABCD ( AC<BD). Gọi E,F thứ tự là các điểm thuộc BD .Sao cho BE=EF=FD.
a, Chứng minh AECF là hình bình hành
b,Kẻ CE;CF cắt AB;AD thứ tự tại M,Q. Kẻ AE,AF cắt CB,CD thứ tự tại N Và P. Chứng minh tứ giác MNPQ là hình bình hành
c,Chứng minh AB² + BC² + CD² + DA² = AC² + BD²
Theo dõi (0) 1 Trả lời -
Chứng minh tứ giác AFCE là hình bình hành biết hình bình hành ABCD có E là trung điểm AB
bởi thu hằng
31/05/2019
Cho hình bình hành ABCD, gọi E là trung điểm AB, F là trung điểm CD.
a) Chứng minh: Tứ giác AFCE là hình bình hành.
b) Hạ AK vuông góc BD tại K, CH vuông góc BD tại H. C/m CK song song AH
Giaỉ giúp mik nhé. ^^
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 79 trang 89 SBT Toán 8 Tập 1
Bài tập 80 trang 89 SBT Toán 8 Tập 1
Bài tập 82 trang 90 SBT Toán 8 Tập 1
Bài tập 83 trang 90 SBT Toán 8 Tập 1
Bài tập 84 trang 90 SBT Toán 8 Tập 1
Bài tập 85 trang 90 SBT Toán 8 Tập 1
Bài tập 86 trang 90 SBT Toán 8 Tập 1
Bài tập 87 trang 90 SBT Toán 8 Tập 1
Bài tập 88 trang 90 SBT Toán 8 Tập 1
Bài tập 89 trang 91 SBT Toán 8 Tập 1
Bài tập 90 trang 91 SBT Toán 8 Tập 1
Bài tập 91 trang 91 SBT Toán 8 Tập 1
Bài tập 7.1 trang 91 SBT Toán 8 Tập 1
