Giải bài 45 tr 92 sách GK Toán 8 Tập 1
Cho hình bình hành ABCD (AB > BC). Tia phân giác của góc D cắt AB ở E, tia phân giác của góc B cắt CD ở F.
a) Chứng minh rằng DE // BF.
b) Tứ giác DEBF là hình gì? Vì sao ?
Hướng dẫn giải chi tiết
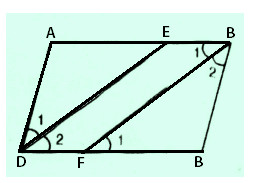
Câu a:
Ta có :
\(\widehat{B}=\widehat{D}\) (Vì ABC D là hình hành)
\(\widehat{B_1}=\widehat{B_2}=\frac{\widehat{B}}{2}\) (BF là tia phân giác góc B)
\(\widehat{D_1}=\widehat{D_2}=\frac{\widehat{D}}{2}\) (DE là tia phân giác góc D)
⇒\(\widehat{D_2}=\widehat{B_1}\) (1)
Ta lại có AB // CD (Vì ABCD là hình bình hành)
Cũng có nghĩa BE // CF
⇒\(\widehat{B_1}=\widehat{F_1}\) (2) (Vì là 2 góc so le trong)
Mà \(\widehat{D_1},\widehat{F_1}\) là cặp góc đồng vị
Do đó DE // BF ( có hai góc đồng vị bằng nhau)
Câu b:
Tứ giác DEBF có:
DE // BF (chứng minh ở câu a)
BE // DF (vì AB // CD)
Nên theo đình nghĩa DEBF là hình bình hành.
-- Mod Toán 8 HỌC247
-
Bài 88* trang 90 sách bài tập toán 8 tập 1
bởi Lê Nhật Minh
13/10/2018
Bài 88* (Sách bài tập - trang 90)
Cho tam giác ABC. Ở phía ngoài tam giác, vẽ các tam giác vuông cân tại A là ABD, ACE. Vẽ hình bình hành ADIE. Chứng minh rằng :
a) \(IA=BC\)
b) \(IA\perp BC\)
Theo dõi (0) 1 Trả lời -
Bài 87* trang 90 sách bài tập toán 8 tập 1
bởi Lê Viết Khánh
13/10/2018
Bài 87* (Sách bài tập - trang 90)
Cho hình bình hành ABCD có \(\widehat{A}=\alpha>90^0\). Ở phía ngoài hình bình hành vẽ các tứ giác đều ADF, ABE
a) Tính \(\widehat{EAF}\)
b) Chứng minh rằng tam giác CEF là tam giác đều
Theo dõi (0) 1 Trả lời -
Bài 86* trang 90 sách bài tập toán 8 tập 1
bởi Sam sung
13/10/2018
Bài 86* (Sách bài tập - trang 90)
Cho hình bình hành ABCD và đường thẳng xy không có điểm chung với hình bình hành. Gọi AA', BB' CC', DD' là các đường vuông góc kẻ từ A, B, C, D đến đường thẳng xy. Tìm mối liên hệ độ dài giữa AA', BB', CC', DD' ?
Theo dõi (0) 1 Trả lời -
Bài 85* trang 90 sách bài tập toán 8 tập 1
bởi sap sua
13/10/2018
Bài 85* (Sách bài tập - trang 90)
Cho hình bình hành ABCD. Qua C kẻ đường thẳng xy chỉ có một điểm chung C với hình bình hành. Gọi AA', BB', DD' là các đường vuông góc kẻ từ A, B, D đến đường thẳng xy.
Chứng minh rằng :
\(AA'=BB'+DD'\)
Theo dõi (0) 1 Trả lời -
Bài 84 trang 90 sách bài tập toán 8 tập 1
bởi Trần Hoàng Mai
13/10/2018
Bài 84 (Sách bài tập - trang 90)
Trên hình 11, cho ABCD là hình bình hành.
.jpg)
Chứng minh rằng :
a) EGFH là hình bình hành
b) Các đường thẳng AC, BD, EF, GH đồng quy
Theo dõi (0) 1 Trả lời
Được đề xuất cho bạn
