Giải bài 82 tr 90 sách BT Toán lớp 8 Tập 1
Trên hình 10, cho ABCD là hình bình hành. Chứng minh rằng AE // CF.
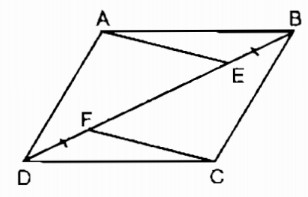
Hướng dẫn giải chi tiết
Hướng dẫn giải
Sử dụng kiến thức:
+) Trong hình bình hành, hai đường chéo cắt nhau tại trung điểm của mỗi đường.
+) Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.
Lời giải chi tiết

Gọi O là giao điểm của AC và BD, ta có:
(tính chất hình bình hành)
Xét ∆ AEB và ∆ CFD :
AB = CD (tính chất hình bình hành)
\(\widehat {ABE} = \widehat {CDF}\) (so le trong)
BE = DF (gt)
Do đó: ∆ AEB = ∆ CFD (c.g.c)
⇒ BE = DF
Ta có: OB = OE + BE
OD = OF + DF
Suy ra: OE = OF
Suy ra: Tứ giác AECF là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường) // CF
-- Mod Toán 8 HỌC247
-


Cho hình bình hành ABCD, AD = 2AB. Từ C vẽ CE vuông góc với AB ( E thuộc AB). Nối E với trung điểm M của AD. T ừ M vẽ MF vuông góc với CE, MF cắt BC tại N.
a/ tứ giác MNCD là hình gì
b/ Tam giác EMC là tam giác gì?
c/ Chứng minh góc BAD = 2 AEM
Theo dõi (0) 1 Trả lời -


Chứng minhdấu hiệu nhận biết hình bình hành
4. Tứ giác có các góc đối bằng nhau là hình bình hành
Theo dõi (0) 1 Trả lời -


Chứng minh HTRY là hình bình hành biết E là trung điểm của MU , I là trung điểm của P
bởi Tran Chau
 31/05/2019
31/05/2019
Cho tứ giác MUPQ, E là trung điểm của MU , I là trung điểm của PQ. Gọi H, T, R, Y lần lượt là trung điểm của MI, EP, UI, EQ. Chứng minh HTRY là hình bình hành.
Theo dõi (0) 1 Trả lời -


Chứng minh tứ giác MNPQ là hình bình hành biết tứ giác ABCD có E là trung điểm AB, F là trung điểm của CD
bởi Ban Mai
 31/05/2019
31/05/2019
Cho tứ giác ABCD có E là trung điểm AB, F là trung điểm của CD. Gọi M,N,P,Q theo thứ tự là trung điểm của AF, CE, BF, DE. chứng minh tứ giác MNPQ là hình bình hành
Theo dõi (0) 1 Trả lời -


Chứng minh AE.CD = BN.DE biết hình vuông ABCD và điểm M nằm trên đường chéo BD
bởi Lê Nhật Minh
 31/05/2019
31/05/2019
Cho hình vuông ABCD và điểm M nằm trên đường chéo BD Kẻ m m F lần lượt vuông góc với AB và AB E thuộc AB E thuộc AB AC Chứng minh rằng AE = SB Chứng minh rằng tam giác AD bằng tam giác d e f C D Gọi N là giao điểm c f và D E Chứng minh rằng AE nhân CD = BN nhân DE
Theo dõi (0) 1 Trả lời -


Chứng minh IA vuông góc BC ở phía ngoài tam giác ABC vẽ các tam giác vuông cân tại A
bởi My Hien
 31/05/2019
31/05/2019
Cho tam giác ABC. Ở phía ngoài tam giác, vẽ các tam giác vuông cân tại A là ABD,ACE. Vẽ hình bình hành ADIE. Chứng minh rằng:
a) IA=BC b) IA vuông góc BCTheo dõi (0) 1 Trả lời -


Chứng minh tứ giác BEDF là hình bình hành biết hình bình hành ABCD có AC giao BD tại O trên AC
bởi Ha Ku
 31/05/2019
31/05/2019
bài 1: cho hình bình hành ABCD có AC giao BD tại O trên AC lấy 2 điểm E,F scho AE=EF=FC ,C/M
a) tứ giác BEDF là hình bình hành
b) DF giao BC tại M , c/m DF=2FM
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 80 trang 89 SBT Toán 8 Tập 1
Bài tập 81 trang 90 SBT Toán 8 Tập 1
Bài tập 83 trang 90 SBT Toán 8 Tập 1
Bài tập 84 trang 90 SBT Toán 8 Tập 1
Bài tập 85 trang 90 SBT Toán 8 Tập 1
Bài tập 86 trang 90 SBT Toán 8 Tập 1
Bài tập 87 trang 90 SBT Toán 8 Tập 1
Bài tập 88 trang 90 SBT Toán 8 Tập 1
Bài tập 89 trang 91 SBT Toán 8 Tập 1
Bài tập 90 trang 91 SBT Toán 8 Tập 1
Bài tập 91 trang 91 SBT Toán 8 Tập 1
Bài tập 7.1 trang 91 SBT Toán 8 Tập 1





