Giải bài 75 tr 89 sách BT Toán lớp 8 Tập 1
Cho hình bình hành ABCD. Tia phân giác của góc A cắt CD ở M. Tia phân giác của góc C cắt AB ở N. Chứng minh rằng AMCN là hình bình hành.
Hướng dẫn giải chi tiết
Hướng dẫn giải
Sử dụng kiến thức: Trong hình bình hành, hai góc đối bằng nhau.
Dấu hiệu nhận biết: Tứ giác có các cạnh đối song song là hình bình hành.
Lời giải chi tiết
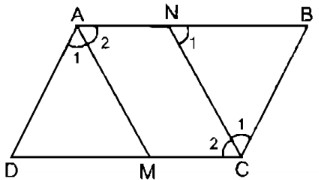
Vì ABCD là hình bình hành nên \(\widehat A = \widehat C\) (tính chất hình bình hành)
\( \displaystyle {\widehat A_2} = {1 \over 2}\widehat A\) (do AM là tia phân giác của góc BAD)
\(\displaystyle {\widehat C_2} = {1 \over 2}\widehat C \) (do CN là tia phân giác của góc BCD)
Suy ra: \(\widehat A_2=\widehat C_2\) (vì \(\widehat A = \widehat C)\)
Lại có \(AB // CD\;\;\) (do ABCD là hình bình hành)
Nên \(AN // CM \;\;(1)\)
Mà \({\widehat N_1} = {\widehat C_2}\) (so le trong)
Suy ra: \({\widehat A_2} = {\widehat N_1}\)
\(⇒ AM // CN \) ( vì có các cặp góc ở vị trí đồng vị bằng nhau) \((2)\)
Từ \((1)\) và \((2)\) suy ra: Tứ giác \(AMCN\) là hình bình hành ( theo định nghĩa)
-- Mod Toán 8 HỌC247
-
Cho tứ giác ABCD Là hình bình hành góc A trừ B=80 tính số đo các góc của tứ giác ABCD
bởi Nguyễn Bình
21/11/2019
Cho tứ giác ABCD là hình bình hành biết A trừ B = 80 tính số đo các gócTheo dõi (0) 3 Trả lời -
Cho hình thang cân abcd có DC=2AB. Gọi M là trung điểm của cạnh DC. N là điểm đối xứng với A qua DC.
a) Chứng minh tứ giác ABCM là hình bình hành
b) Chứng minh tứ giác AMND là hình thoi
Theo dõi (1) 5 Trả lời -
Cho tứ giác lồi ABCD có 2 đường chéo AC và BD cắt nhau tại P. Biết rằng góc DAC = 90, và 2 lần góc ADB = 1 lần góc ACB. Chứng minh rằng nếu góc DBC + 2 lần góc ADC = 180 độ thì 2AP=BP
Theo dõi (1) 3 Trả lời -
Cho hình bình hành abcd có tâm O . Qua o kẻ đường thẳng lần lượt cắt ab,cd tại m và n. Cm o là trug điểm mn
Theo dõi (0) 1 Trả lời -
Chứng minh tứ giác AEBC là hình bình hành
bởi Hoa Lan
31/05/2019
Cho hình hình hành ABCD. Gọi E là điểm đối xứng với D qua điểm A, gọi F là điểm đối xứng với D qua điểm C.
a) Chứng minh rằng tứ giác AEBC là hình bình hành
b)Chứng minh rằng tứ giác ABFC là hình bình hành
c)Chứng minh rằng E đối xứng với F qua B
Khỏi vẽ hình cũng được
Theo dõi (0) 1 Trả lời -
Chứng minh E và F đối xứng với nhau qua C biết hình bình hành ABCD có E đối xứng với A qua B
bởi Anh Trần
31/05/2019
cho hình bình hành ABCD E đối xứng với A qua B , F đối xứng với A qua D
chứng minh: E và f đối xứng với nhau qua C
LÀM ƠN GIÚP MÌNH VỚI MÌNH ĐANG CẦN GẤP
Theo dõi (0) 1 Trả lời -
Chứng minh AECF là hình bình hành biết hình bình hành ABCD có E là trung điểm của cạnh AB
bởi na na
31/05/2019
cho hình bình hành ABCD gọi E là trung điểm của cạnh AB ,F là trung điểm cạnh CD .
a: chứng minh AECF là hình bình hành
b: DE cắt AC ở I ,BF cắt AC ở K chứng minh AI=IK=KC
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 73 trang 89 SBT Toán 8 Tập 1
Bài tập 74 trang 89 SBT Toán 8 Tập 1
Bài tập 76 trang 89 SBT Toán 8 Tập 1
Bài tập 77 trang 89 SBT Toán 8 Tập 1
Bài tập 78 trang 89 SBT Toán 8 Tập 1
Bài tập 79 trang 89 SBT Toán 8 Tập 1
Bài tập 80 trang 89 SBT Toán 8 Tập 1
Bài tập 81 trang 90 SBT Toán 8 Tập 1
Bài tập 82 trang 90 SBT Toán 8 Tập 1
Bài tập 83 trang 90 SBT Toán 8 Tập 1
Bài tập 84 trang 90 SBT Toán 8 Tập 1
Bài tập 85 trang 90 SBT Toán 8 Tập 1
Bài tập 86 trang 90 SBT Toán 8 Tập 1
Bài tập 87 trang 90 SBT Toán 8 Tập 1
Bài tập 88 trang 90 SBT Toán 8 Tập 1
Bài tập 89 trang 91 SBT Toán 8 Tập 1
Bài tập 90 trang 91 SBT Toán 8 Tập 1
Bài tập 91 trang 91 SBT Toán 8 Tập 1
Bài tập 7.1 trang 91 SBT Toán 8 Tập 1
