Bài tập 87 trang 90 SBT Toán 8 Tập 1

Hướng dẫn giải

Sử dụng kiến thức:

+) Trong hình bình hành, hai góc kề một cạnh bù nhau. 

+) Trong tam giác đều, các cạnh bằng nhau, các góc bằng nhau và bằng \(60^o.\)

+) Trong hình bình hành, hai góc đối bằng nhau.

+) Tam giác có cạnh bằng nhau là tam giác đều.

Lời giải chi tiết

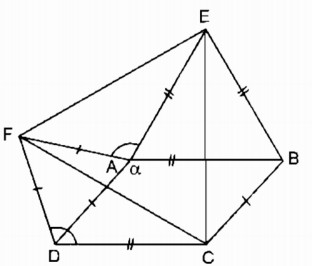
a. Vì \(\eqalign{  & \widehat {BAD} + \widehat {BAE} + \widehat {EAF} + \widehat {FAD} = {360^0}  \cr  &  \Rightarrow \widehat {EAF} = {360^0} - \left( {\widehat {BAD} + \widehat {BAE} + \widehat {FAD}} \right) \cr} \)

mà \(\widehat {BAD} = \alpha \) (gt)

\(\widehat {BAE} = {60^0}\) (∆ BAE đều)

\(\widehat {FAD} = {60^0}\) (∆ FAD đều)

nên \(\widehat {EAF} = {360^0} - \left( {\alpha  + {{60}^0} + {{60}^0}} \right) = {240^0} - \alpha \)

b. Ta có: \(\widehat {ADC} + \widehat {BAD} = {180^0}\) (hai góc trong cùng phía bù nhau)

\(\eqalign{  &  \Rightarrow \widehat {ADC} = {180^0} - \widehat {BAD} = {180^0} - \alpha   \cr  & \widehat {CDF} = \widehat {ADC} + \widehat {ADF} = {180^0} - \alpha  + {60^0} = {240^0} - \alpha  \cr} \)

Suy ra: \(\widehat {CDF} = \widehat {EAF}\)

Xét ∆ AEF và ∆ DCF:

AF = DF (vì ∆ ADF đều)

AE = DC (vì cùng bằng AB)

\(\widehat {CDF} = \widehat {EAF}\) (chứng minh trên)

Do đó ∆ AEF = ∆ DCF (c.g.c) ⇒ EF = CF (1)

\(\widehat {ADC} = \widehat {ABC}\) (tính chất hình bình hành)

\(\widehat {CBE} = \widehat {ABC} + {60^0} = \widehat {ADC} + {60^0} = {180^0} - \alpha  + {60^0} = {240^0} - \alpha \)

Xét ∆ BCE và ∆ DCF:

BE = CD (vì cùng bằng AB)

\(\widehat {CBE} = \widehat {CDF} = {240^0} - \alpha \)

BC = DF (vì cùng bằng AD)

Do đó: ∆ BCE = ∆ DFC (c.g.c) ⇒ CE = CF (2)

Từ (1) và (2) suy ra : EF = CF = CE. Vậy ∆ ECF đều.

-- Mod Toán 8 HỌC247