Giải bài 88 tr 90 sách BT Toán lớp 8 Tập 1
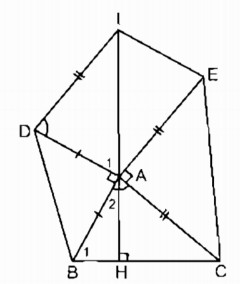
Cho tam giác \(ABC.\) Ở phía ngoài tam giác, vẽ các tam giác vuông cân tại \(A\) là \(ABD, ACE.\) Vẽ hình bình hành \(ADIE.\) Chứng minh rằng:
\(a)\) \(IA = BC.\)
\(b)\) \(IA ⊥ BC.\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
\(a)\) Quy về bài toán chứng minh hai tam giác bằng nhau.
\(b)\) Quy về chứng minh \(\widehat {AHB} = {90^0}\)
+) Tổng ba góc trong một tam giác bằng \(180^o\)
Lời giải chi tiết
a. \(\widehat {BAC} + \widehat {BAD} + \widehat {DAE} + \widehat {EAC} = {360^0}\)
\(\widehat {BAD} = {90^0},\widehat {EAC} = {90^0}(gt)\)
Suy ra: \(\widehat {BAC} + \widehat {DAE} = {180^0}\) (1)
AE // DI (gt)
⇒ \(\widehat {ADI} + \widehat {DAE} = {180^0}\) (hai góc trong cùng phía) (2)
Từ (1) và (2) suy ra:
Xét ∆ ABC và ∆ DAI :
AB = AD (gt)
\(\widehat {BAC} = \widehat {ADI}\) (chứng minh trên)
AC = DI (vì cùng bằng AE)
Do đó: ∆ ABC = ∆ DAI (c.g.c) ⇒ IA = BC
b. ∆ ABC = ∆ DAI ( chứng minh trên) \( \Rightarrow {\widehat A_1} = {\widehat B_1}\) (3)
Gọi giao điểm IA và BC là H.
Ta có: \({\widehat A_1} + \widehat {BAD} + {\widehat A_2} = {180^0}\) (kề bù)
mà \(\widehat {BAD} = {90^0}(gt) \Rightarrow {\widehat A_1} + {\widehat A_2} = {90^0}\) (4)
Từ (3) và (4) suy ra: \({\widehat B_1} = {\widehat A_2} = {90^0}\)
Trong ∆ AHB ta có: \(\widehat {AHB} + \widehat {{B_1}} + {\widehat A_2} = {180^0}\)
Suy ra \(\widehat {AHB} = {90^0} \Rightarrow AH \bot BC\) hay IA ⊥ BC
-- Mod Toán 8 HỌC247
-


Cho tam giác ABC ,E là một điểm bất kì thuộc cạnh AC .Qua E kẻ đường thẳng song song với BA cắt BC ở D và đường thảng song song Với BC cắt AB ở F .Giả sử là AE=BF .Chứng minh
a)Tam giác ADE cân
b) AD phân giác
Theo dõi (0) 1 Trả lời -


Chứng minh MP, EQ và FN đồng quy
bởi Sasu ka
 31/05/2019
31/05/2019
Cho hình bình hành MNPQ. QUa đỉnh P kẻ đường thẳng song song với QN cắt MN tại F. Chứng minh MP, EQ và FN đồng quy
Theo dõi (0) 1 Trả lời -


Cho hình bình hành ABCD có AB < AD. Tia phân giác của góc A cắt BC ở I, tia phân giác của góc C cắt AD tại K. Chứng minh:
1) Tam giác ABI là tam giác cân
2) So sánh \(\widehat{BIA}\) và \(\widehat{KCB}\)
3)Tứ giác AICK là hình bình hành
Theo dõi (0) 1 Trả lời -


Chứng minh MNEF là hình bình hành biết tam giác ABC có các đường trung tuyến BE, CF và trọng tâm G
bởi Phan Thiện Hải
 31/05/2019
31/05/2019
Cho tam giác ABC có các đường trung tuyến BE, CF và trọng tâm G. Gọi M và N lần lươt là trung điểm của BG và CG.
1) Chứng minh EF // MN, EF = MN.
2) Chứng minh MNEF là hình bình hành.
Theo dõi (0) 1 Trả lời -


Chứng minh tứ giác MNPQ là hình bình hành biết tam giác ABCD có M, N, P, Q lần lượt là trung điểm của AB, AC, CD, BD
bởi thi trang
 31/05/2019
31/05/2019
Cho tứ giác ABCD có M, N, P, Q lần lượt là trung điểm của AB, AC, CD, BD.
1) Chứng minh rằng MN // BC, MN = \(\dfrac{BC}{2}\)
2) Chứng minh MN // PQ , MN = PQ
3) Chứng minh tứ giác MNPQ là hình bình hành
Theo dõi (0) 1 Trả lời -


Cho tam giác ABCcó đường phân giác AD .Qua D kẻ đường thằng song song với AB cắt AC ở E . Qua Ekẻ đường thẳng song song với BC cắt AB ở F.
C/M : AE = BF.
Theo dõi (0) 1 Trả lời -


3) Cho tam giác ABC có D, E, F theo thứ tự là trung điểm của AB, AC, BC. Chứng minh BDEF là hình bình hành và suy ra góc B bằng góc DEF.
Theo dõi (0) 1 Trả lời





