Bài tập 49 trang 93 SGK Toán 8 Tập 1

29 BT SGK

Giải bài 49 tr 93 sách GK Toán 8 Tập 1

Cho hình bình hành ABCD. Gọi I, K theo thứ tự là trung điểm của CD, AB. Đường chéo BD cắt AI, CK theo thứ tự ở M và N. Chứng minh rằng:

a) AI // CK

b) DM = MN = NB

Hình học 8 Bài 7 Trắc nghiệm Hình học 8 Bài 7 Giải bài tập Hình học 8 Bài 7

Hướng dẫn giải chi tiết

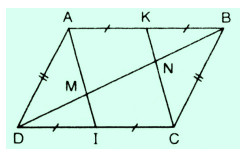
Câu a:

Tứ giác ABCD có AB = CD, AD = BC nên là hình bình hành.

Tứ giác AICK có AK // IC, AK = IC nên là hình bình hành.

Do đó AI // CK

Câu b:

∆DCN có DI = IC, IM // CN.

(vì AI // CK) nên suy ra DM = MN

Chứng minh tương tự đối với ∆ABM ta có MN = NB.

Vậy DM = MN = NB

-- Mod Toán 8 HỌC247

Nếu bạn thấy hướng dẫn giải Bài tập 49 trang 93 SGK Toán 8 Tập 1 HAY thì click chia sẻ

YOMEDIA

Chứng minh OE.AD = OF.AB?

bởi Ngô Việt Hà 24/06/2020

Hình bình hành ABCD có O thuộc đường chéo AC. Từ O kẻ OE vuông góc với AB, OF vuông góc với AD. CMR: OE.AD=OF.AB

Hôm nay em thi học kì câu cuối cùng nó như thế này mọi người ạ. Đề nó cho khó hiểu cực

Theo dõi (1) 0 Trả lời
Tìm điều kiện để hình bình hành trên là hình chữ nhật?

bởi Nguyễn Văn Thanh 08/06/2020

Giúp mh vs mh đg gấp

Cho tam giác ABC có E,F,G lần lượt là trung điểm của AB,AC,BC gọi M là trọng tâm của tam giác lấy H đối xứng với M qua G cm tứ giác BMCH là hình bình hành. tìm điều kiện để hình bình hành trên là hình chữ nhật

Theo dõi (0) 0 Trả lời
Chứng minh tứ giác AHCG là hình bình hành biết hình bình hành ABCD có 2 đường chéo AC và BD cắt nhau tại O

bởi Nguyen Giang 13/04/2020

Cho hình bình hành ABCD có 2 đường chéo AC và BD cắt nhau tại O. Trên AB và CD lấy 2 đoạn AE = CF, trên AD và BC lấy 2 đoạn AG = CH. Chứng minh rằng: a, Tứ giác AHCG là hình bình hành b, Tứ giác EHFG là hình bình hành c, AC, BD, GH , EF đồng quy

Theo dõi (0) 0 Trả lời
Chứng minh tam giác ADM=tam giác CBN biết hình bình hành ABCD, K, I lần lượt là trung điểm của các cạnh AB và CD

bởi trâm anh 10/04/2020

Cho hình bình hành ABCD.Gọi KI lần lượt là trung điểm của các cạnh AB và CD gọi M và N lần lượt là giao điểm của AI và CK với BD chứng minh a) tam giác ADM=tam giác CBN b) góc MAC = góc NCA , IM//CN c) DM=MN=NB

Theo dõi (0) 0 Trả lời
ABMN là hình gì? Vì sao?

bởi Hoàng Trang 07/04/2020

Cho hình bình hành ABCD

Theo dõi (0) 1 Trả lời
Tính các góc còn lại của hình bình hành ABCD biết góc A=120 độ

bởi Thủy Nguyễn Thị 05/04/2020

Cho hình bình hành ABCD có góc A =120° .các góc còn lại có giá trị bao nhiêu?

Theo dõi (0) 3 Trả lời
Cho hình bình hành ABCD. Gọi E là trung điểm của cạnh AB, F là trung điểm của cạnh CD. Chứng minh rằng hai đoạn thẳng DE và BF chia đường chéo AC thành ba đoạn bằng nhau.

bởi Nấm Lùn Cute 23/03/2020

Cho hình bình hành ABCD. Gọi E là trung điểm của cạnh AB, F là trung điểm của cạnh
CD. Chứng minh rằng hai đoạn thẳng DE và BF chia đường chéo AC thành ba đoạn bằng
nhau.
HD: Gọi M, N lần lượt là giao điểm của DE và BF với AC. Chứng minh: AM = MN = NC.

Theo dõi (0) 1 Trả lời