Bài tập 89 trang 91 SBT Toán 8 Tập 1

Hướng dẫn giải

+) Cách dựng: Nêu thứ tự từng bước dựng hình, đồng thời thể hiện các nét dựng trên hình vẽ.

+) Chứng minh: Bằng lập luận để chứng tỏ rằng với cách dựng trên, hình đã dựng thỏa mãn các điều kiện của đề bài nêu ra.

+) Biện luận: Xem xét khi nào bài toán dựng được và dựng được bao nhiêu hình thỏa mãn đề bài

Biện luận: Ta luôn dựng được một tam giác thỏa mãn điều kiện của đề bài.

Lời giải chi tiết

Cách dựng:

Dựng ∆ ABD có AB = 2cm, \(\widehat A = {110^0}\), AD = 3cm

-  Dựng tia Bx // AD

-  Dựng tia Dy // AB cắt Bx tại C

Ta có hình bình hành ABCD cần dựng

Chứng minh: AB // CD, AD // BC nên tứ giác ABCD là hình bình hành.

Ta lại có AB = 2cm, \(\widehat A = {110^0}\) , AD = 3cm. Bài toán có một nghiệm hình.

b.

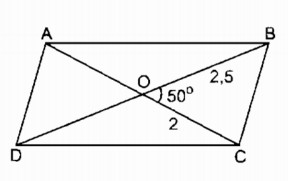
Cách dựng:

-  Dựng ∆ OBC có OC = 2cm, OB = 2,5cm , \(\widehat O = {50^0}\)

-  Trên tia đối tia OC lấy điểm A sao cho OA = OC = 2cm

-  Trên tia đối tia OB lấy điểm D sao cho AD = OB = 2,5cm

Nối AB, BC, CD, AD ta có hình bình hành ABCD cần dựng

Chứng minh: Tứ giác ABCD có OA = OC, OB = OD nên nó là hình bình hành vì có hai đường chéo cắt nhau tại trung điểm mỗi đường.

Có AC = 4cm, BD = 5cm, \(\widehat {BOC} = {50^0}\)

Bài toán có một nghiệm hình.

-- Mod Toán 8 HỌC247