Giải bài 3 tr 104 sách GK Toán Hình lớp 11
Cho hình chóp S.ABCD có đáy là hình thoi ABCD tâm O và có SA = SB = SC = SD. Chứng minh rằng:
a) Đường thẳng SO vuông góc với mặt phẳng (ABCD)
b) Đường thẳng AC vuông góc với mặt phẳng (SBD) và đường thẳng BD vuông góc với mặt phẳng (SAC)
Hướng dẫn giải chi tiết
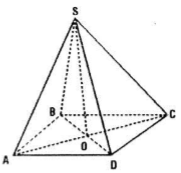
Câu a:
Vì SA = SC ⇒ tam giác SAC cân đỉnh S, mặt khác O là trung điểm của AC
\(\Rightarrow SO\perp AC\)
Tương tự \(SO\perp BD\)
Suy ra \(SO\perp (ABCD)\) (đpcm)
Câu b:
* Ta có \(SO\perp AC\) và \(BD\perp AC\) (hai đường chéo của hình thoi)
\(\Rightarrow AC\perp (ABD)\)
+ \(AC\perp BD\) (đường chéo hình thoi)
+ \(AC\perp SO\)
+ BD cắt SO trong (SBD)
* Ta có:
+ \(BD\perp AC\)
+\(BD\perp SO\)
+ AC cắt SO trong (SAC)
\(\Rightarrow BD\perp (SAC)\)
-- Mod Toán 11 HỌC247
-


Tập hợp các điểm cách đều các đỉnh của một tam giác là đường thẳng vuông góc với mặt phẳng chứa tam giác đó và đi qua:
bởi minh thuận
 25/01/2021
25/01/2021
A. Tâm đường tròn ngoại tiếp tam giác đó.
B. Trọng tâm tam giác đó.
C. Tâm đường tròn nội tiếp tam giác đó.
D. Trực tâm tam giác đó.
Theo dõi (0) 1 Trả lời -


Chỉ ra mệnh đề sai trong các mệnh đề sau:
bởi Mai Bảo Khánh
 25/01/2021
25/01/2021
A. Hai đường thẳng chéo nhau và vuông góc với nhau. Khi đó có một và chỉ một mp chứa đường thẳng này và vuông góc với đường thẳng kia.
B. Qua một điểm O cho trước có một mặt phẳng duy nhất vuông góc với một đường thẳng Δ cho trước.
C. Qua một điểm O cho trước có một và chỉ một đường thẳng vuông góc với một đường thẳng cho trước.
D. Qua một điểm O cho trước có một và chỉ một đường thẳng vuông góc với một mặt phẳng cho trước.
Theo dõi (0) 1 Trả lời -


Cho hai đường thẳng a, b và mp (P) . Chỉ ra mệnh đề đúng trong các mệnh đề sau:
bởi May May
 26/01/2021
26/01/2021
A. Nếu a // (P) và b ⊥ a thì b // (P) .
B. Nếu a // (P) và b ⊥ (P) thì a ⊥ b .
C. Nếu a // (P) và b ⊥ a thì b ⊥ (P).
D. Nếu a ⊥ (P) và b ⊥ a thì b // (P).
Theo dõi (0) 1 Trả lời -


A. Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.
B. Có duy nhất một mặt phẳng đi qua một đường thẳng cho trước và vuông góc với một mặt phẳng cho trước.
C. Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.
D. Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.
Theo dõi (0) 1 Trả lời -


Cho a, b, c là các đường thẳng trong không gian. Tìm mệnh đề sai trong các mệnh đề sau.
bởi Mai Bảo Khánh
 26/01/2021
26/01/2021
A. Nếu a ⊥ b và b ⊥ c thì a // c
B. Nếu a vuông góc với mặt phẳng (α) và b // (α) thì a ⊥ b
C. Nếu a // b và b ⊥ c thì c ⊥ a
D. Nếu a ⊥ b , b ⊥ c và a cắt c thì b vuông góc với mặt phẳng (a; c)
Theo dõi (0) 1 Trả lời -


Trong không gian cho đường thẳng Δ không nằm trong mp(P) , đường thẳng Δ được gọi là vuông góc với mp (P) nếu:
bởi Nguyễn Hồng Tiến
 25/01/2021
25/01/2021
A. vuông góc với hai đường thẳng phân biệt nằm trong mp (P)
B. vuông góc với đường thẳng a mà a song song với mp (P)
C. vuông góc với đường thẳng a nằm trong mp (P)
D. vuông góc với mọi đường thẳng nằm trong mp (P)
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 1 trang 104 SGK Hình học 11
Bài tập 2 trang 104 SGK Hình học 11
Bài tập 4 trang 105 SGK Hình học 11
Bài tập 5 trang 105 SGK Hình học 11
Bài tập 6 trang 105 SGK Hình học 11
Bài tập 7 trang 105 SGK Hình học 11
Bài tập 8 trang 105 SGK Hình học 11
Bài tập 3.16 trang 145 SBT Hình học 11
Bài tập 3.17 trang 145 SBT Hình học 11
Bài tập 3.18 trang 145 SBT Hình học 11
Bài tập 3.19 trang 145 SBT Hình học 11
Bài tập 3.20 trang 145 SBT Hình học 11
Bài tập 3.21 trang 145 SBT Hình học 11
Bài tập 12 trang 102 SGK Hình học 11 NC
Bài tập 13 trang 102 SGK Hình học 11 NC
Bài tập 14 trang 102 SGK Hình học 11 NC
Bài tập 15 trang 102 SGK Hình học 11 NC
Bài tập 16 trang 103 SGK Hình học 11 NC
Bài tập 17 trang 103 SGK Hình học 11 NC
Bài tập 18 trang 103 SGK Hình học 11 NC





