Giải bài 3.16 tr 145 SBT Hình học 11
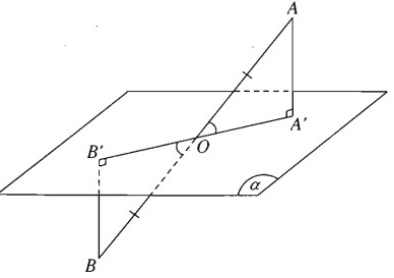
Một đoạn thẳng AB không vuông góc với mặt phẳng (α) cắt mặt phẳng này tại trung điểm O của đoạn thẳng đó. Các đường thẳng vuông góc với (α) qua A và B lần lượt cắt mặt phẳng (α) tại A' và B'.
Chứng minh ba điểm A', O, B' thẳng hàng và AA' = BB'
Hướng dẫn giải chi tiết
\(\left\{ \begin{array}{l}
AA' \bot \left( \alpha \right)\\
BB' \bot \left( \alpha \right)
\end{array} \right. \Rightarrow AA'\parallel BB'\)
Mặt phẳng (AA', BB') xác định bởi hai đường thẳng song song (AA', BB') cắt mặt phẳng (α) theo giao tuyến qua O, A', B'. Do đó ba điểm O, A', B' thẳng hàng.
Hai tam giác vuông OAA'và OBB' bằng nhau vì có một cạnh huyền và một góc nhọn bằng nhau nên từ đó ta suy ra AA' = BB'.
-- Mod Toán 11 HỌC247
-
Chứng minh CD vuông góc với mặt phẳng (SAD)?
bởi Nguyễn Trà My
17/06/2020
Giúp em với ạ
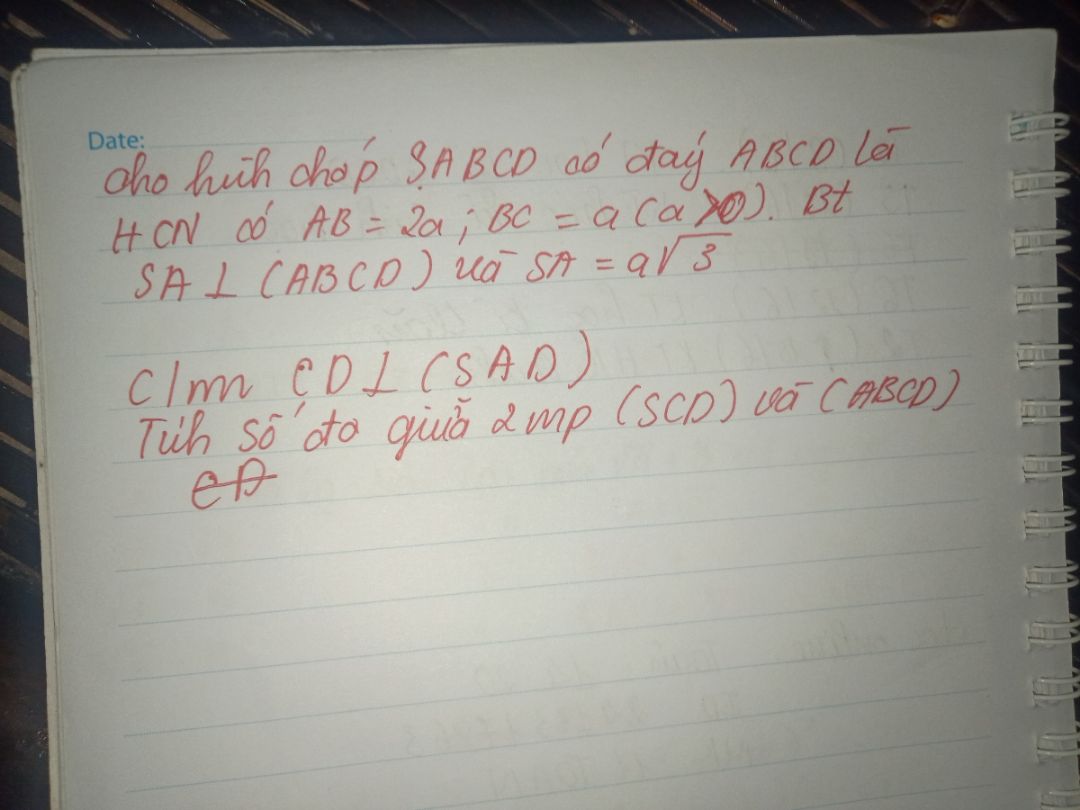Theo dõi (0) 4 Trả lời -
Tính góc giữa đường thẳng SC và mặt phẳng (ABCD)??
bởi Liên Ngọc
13/06/2020
Giúp mình với
Theo dõi (1) 4 Trả lời -
Chứng minh BC vuông góc với (SAB)?
bởi Hương Hoàng
13/06/2020
Tự luận
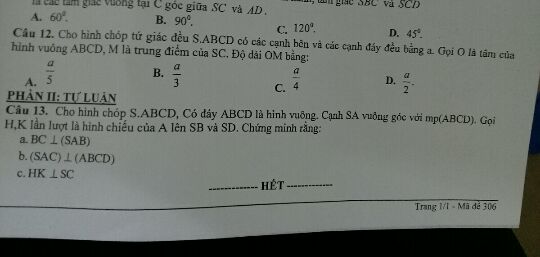Theo dõi (0) 3 Trả lời -
Chứng minh AC vuông góc với (SBD)?
bởi vũ nguyệt
11/06/2020
Hình chóp SABCD có đáy ABCD là hình vuông. SA vuông góc với đáy. Chứng minh AC vuông góc với (SBD)?
Theo dõi (0) 4 Trả lời -
Chứng minh BD vuông góc với (SAC)?
bởi Nguyễn Mai Lan
07/06/2020
Ai giải giúp tui với
Cho hình chóp S ABCD có đáy là hình vuông cạnh 3a .SA vuông góc với đáy SA=6a . Chứng minh rằng :
a) BD vuông góc với (SAC) .
b, chứng minh rằng SAC vuông góc với SBD
Theo dõi (0) 5 Trả lời -
Cho hình chóp SMNP đáy là tam giác đều cạnh bằng 2a. SM vuông góc với đáy. SM= 2a√3. K là trung điểm của NP. J là trung điểm MN chứng minh NP vuông góc với (SKP) và PJ vuông góc với (SMN).
Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 7 trang 105 SGK Hình học 11
Bài tập 8 trang 105 SGK Hình học 11
Bài tập 3.17 trang 145 SBT Hình học 11
Bài tập 3.18 trang 145 SBT Hình học 11
Bài tập 3.19 trang 145 SBT Hình học 11
Bài tập 3.20 trang 145 SBT Hình học 11
Bài tập 3.21 trang 145 SBT Hình học 11
Bài tập 12 trang 102 SGK Hình học 11 NC
Bài tập 13 trang 102 SGK Hình học 11 NC
Bài tập 14 trang 102 SGK Hình học 11 NC
Bài tập 15 trang 102 SGK Hình học 11 NC
Bài tập 16 trang 103 SGK Hình học 11 NC
Bài tập 17 trang 103 SGK Hình học 11 NC
Bài tập 18 trang 103 SGK Hình học 11 NC
