Giải bài 8 tr 105 sách GK Toán Hình lớp 11
Cho điểm S không thuộc cùng mặt phẳng (α) có hình chiếu là điểm H. Với điểm M bất kì trên (α) và M không trùng với H, ta gọi SM là đường xiên và đoạn HM là hình chiếu của đường xiên đó. Chứng minh rằng:
a) Hai đường thẳng xiên bằng nhau khi và chỉ khi hai hình chiếu của chúng bằng nhau;
b) Với hai đường xiên cho trước, đường xiên nào lớn hơn thì có hình chiếu lớn hơn và ngược lại đường xiên nào có hình chiếu lớn hơn thì lớn hơn.
Hướng dẫn giải chi tiết
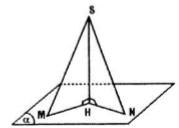
Lấy điểm \(N\not\equiv M\) trên \((\alpha )\)
Câu a:
Giả sử: \(HM=HN\)
Ta thấy tam giác HSM và tam giác HSN có:
HS chung; \(HM=HN; \widehat{SHM}=\widehat{SHN}=90^0\)
Ngược lại nếu SM = SN thì hai tam giác vuông HSM và HSN cũng bằng nhau.
⇒ HM = HN
Vậy HM = HN ⇔ SM = SN (đpcm)
Câu b:
Giả sử \(HM >HN \Leftrightarrow \sqrt{SM^2-SH^2}>\sqrt{SN^2-SH^2}\)
\(\Leftrightarrow SM^2>SN^2\)
\(\Leftrightarrow SM>SN\) (đpcm)
-- Mod Toán 11 HỌC247
-
Cho hình chóp S.ABCD đáy là hình thoi tâm O và SA = SC, SB= SD. Đường thẳng BC vuông góc với đường thẳng
bởi Co Nan
24/01/2021
A. SA
B. SB
C. SC
D. SO
Theo dõi (0) 1 Trả lời -
Cho hình chóp S.ABCD đáy là hình thoi tâm O và SA = SC, SB= SD. Đường thẳng DB không vuông góc với đường thẳng nào sau đây?
bởi Nguyễn Lệ Diễm
25/01/2021
A. AC
B. SA
C. SB
D. SC
Theo dõi (0) 1 Trả lời -
Cho tứ diện ABCD có hai mặt ABC và BCD là hai tam giác cân có chung cạnh đáy BC. Gọi I là trung điểm của canh BC a) Chứng minh rằng BC vuông góc với mặt phẳng (ADI)
bởi Lê Hoàng Thảo Linh
13/01/2021
Cho tứ diện ABCD có hai mặt ABC và BCD là hai tam giác cân có chung cạnh đáy BC. Gọi I là trung điểm của canh BC
a) Chứng minh rằng BC vuông góc với mặt phẳng (ADI)
b) Gọi AH là đường cao của tam giác ADI, chứng minh rằng AH vuông góc với mặt phẳng (BCD)
Theo dõi (0) 2 Trả lời -
Cho A(1;3); B(-1;2) (C): x²+y²-2x+4y+1=0 Điểm C' thuộc C ,sao cho ABCD là hình bình hành tìm quỹ tích D khi điểm C di động trên đường tròn.
bởi Mi Na
09/09/2020
Cho A(1;3); B(-1;2)
(C): x²+y²-2x+4y+1=0
Điểm C' thuộc C ,sao cho ABCD là hình bình hành tìm quỹ tích D khi điểm C di động trên đường tròn. Mọi người giải giúp e vs ạ!
Theo dõi (0) 0 Trả lời -
Tính góc giữa EF và mặt phẳng SAC?
bởi Leo Ckan
26/06/2020
Cho hình chóp S.ABC hình thang vuông tại A, D, AD=CD=a có AB =2a, SA vuông với (ABCD) SA=a. Gọi E, F là trung điểm của SD,BC. Tính góc giữa EF và mặt phẳng SAC?
Theo dõi (0) 0 Trả lời -
Trong không gian hai đường thẳng được gọi là vuông góc với nhau nếu góc giữa của chúng bằng?Theo dõi (0) 4 Trả lời
Bài tập SGK khác
Bài tập 6 trang 105 SGK Hình học 11
Bài tập 7 trang 105 SGK Hình học 11
Bài tập 3.16 trang 145 SBT Hình học 11
Bài tập 3.17 trang 145 SBT Hình học 11
Bài tập 3.18 trang 145 SBT Hình học 11
Bài tập 3.19 trang 145 SBT Hình học 11
Bài tập 3.20 trang 145 SBT Hình học 11
Bài tập 3.21 trang 145 SBT Hình học 11
Bài tập 12 trang 102 SGK Hình học 11 NC
Bài tập 13 trang 102 SGK Hình học 11 NC
Bài tập 14 trang 102 SGK Hình học 11 NC
Bài tập 15 trang 102 SGK Hình học 11 NC
Bài tập 16 trang 103 SGK Hình học 11 NC
Bài tập 17 trang 103 SGK Hình học 11 NC
Bài tập 18 trang 103 SGK Hình học 11 NC
