Bài tập 15 trang 102 SGK Hình học 11 NC
Cho tứ diện ABCD. Tìm điểm O cách đều bốn đỉnh của tứ diện.
Hướng dẫn giải chi tiết
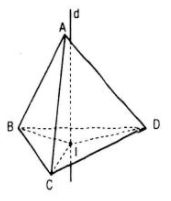
Gọi I là tâm đường tròn ngoại tiếp của ΔBCD
Gọi d là đường thẳng đi qua I và vuông góc với mặt phẳng (BCD)
Theo kết quả bài 14. M \( \in \) d ⇔ MB = MC = MD
(d gọi là trục của đường tròn ngoại tiếp tam giác BCD)
Gọi O là giao điểm của d với mặt phẳng trung trực của AB thì O cách đều bốn đỉnh của tứ diện (O gọi là tâm mặt cầu ngoại tiếp tứ diện ABCD).
-- Mod Toán 11 HỌC247
-
Cho tứ diện S.ABC có ABC là tam giác vuông, SA vuông góc với (ABC).a. Chứng minh 4 mặt tứ diện là tam giác vuông.b. Kẻ AH, AK lần lượt là đường cao của SAB và SAC, HK cắt tia BC tại I. Chứng minh AIC là tam giác vuông.
bởi Hoàng Ngân
22/03/2020
Cho tứ diện S.ABC có ABC là tam giác vuông, SA vuông góc với (ABC).a. Chứng minh 4 mặt tứ diện là tam giác vuông.b. Kẻ AH, AK lần lượt là đường cao của SAB và SAC, HK cắt tia BC tại I. Chứng minh AIC là tam giác vuông.Theo dõi (0) 0 Trả lời -
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 3a, SA vuông góc với (ABCD) có SA=2a. a/ tính BD vuông góc (SAC) b/ Tính góc giữa SC và (ABCD)
bởi Liên Mỹ
17/03/2020
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 3a, SA vuông góc với (ABCD) có SA=2a.
a/ Tính BD vuông góc (SAC)
b/ Tính góc giữa SC và (ABCD)
Theo dõi (0) 1 Trả lời -
Cho hình chóp S.ABCD có SB vuông góc với mặt phẳng (ABCD) và SB=a√3, ABCD là hình thoi cạnh a, có góc A bằng 60 độ. Chứng minh AC vuông góc với mặt phẳng SBD. Cho biết tam giác ABD là tam giác gì? Vì sao?
bởi Quế Anh Nguyễn
14/03/2020
Theo dõi (0) 1 Trả lời -
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại C, SA vuông góc với (ABC). Chứng minh BC vuông góc với (SAC)
bởi Mai Hoàng Thị Thu
04/03/2020
Theo dõi (0) 0 Trả lời -
Cho hình chóp SABCD có đáy ABC là tam giác cân tại C . AC =BC,=a√10 , mặt bên SAB là tam giác để cạnh 2a và nằm trong mặt phẳng vuông góc với đáy . Tính góc giữa đường thẳng SC và mặt phẳng (ABC)
bởi Hoàng Tấn
01/03/2020
Cho hình chóp SABCD có đáy ABC là tam giác cân tại C . AC =BC,=a√10 , mặt bên SAB là tam giác để cạnh 2a và nằm trong mặt phẳng vuông góc với đáy . Tính góc giữa đường thẳng SC và mặt phẳng (ABC)Theo dõi (0) 0 Trả lời -
Tính góc giữa SD và (ABCD) biết hình chóp S.ABCD đáy là ABCD là hình chữ nhật tâm O, cạnh AB=a, AC=a căn 5
bởi Thảo La Vi
22/02/2020
Cho hình chóp S.ABCD đáy là ABCD là hình chữ nhật tâm O, cạnh AB=a, AC=a căn 5. SO vuông góc với mặt đáy và SO=2a. Tính góc giữa:
a) SD và (ABCD)
b) SO và (ABCD)
Theo dõi (0) 1 Trả lời
