Giải bài 7 tr 105 sách GK Toán Hình lớp 11
Cho tứ diện SABC có cạnh SA vuông góc với mặt phẳng (ABC) và có tam giác ABC vuông tại B. Trong mặt phẳng (SAB) kẻ từ AM vuông góc với SB tại M. Trên cạnh SC lấy điểm N sao cho \(\frac{{SM}}{{SB}} = \frac{{SN}}{{SC}}\) Chứng minh rằng:
a) \(BC \perp (SAC)\) và \(AM \perp (SBC)\);
b) \(SB \perp AN\).
Hướng dẫn giải chi tiết
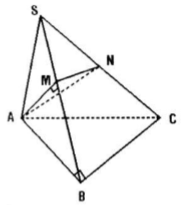
Câu a:
Ta nhận thấy \(SA\perp (ABC)\Rightarrow BC\perp SA\) và \(BC\perp AB\) (giả thiết) suy ra \(BC\perp (SAB)\)
Vì \(\left\{\begin{matrix} BC\perp (SAB)\\ AM\subset (SAB) \end{matrix}\right.\Rightarrow BC\perp AM\)
Lại có \(AM\perp SB\). Suy ra \(AM\perp (SBC)\)
Câu b:
Từ giả thiết \(\frac{SM}{SB}=\frac{SN}{SC}\Rightarrow MN // BC\)
Vì \(BC\perp (SAB)\Rightarrow MN\perp (SBC)\Rightarrow SB\perp MN\)
Vì \(BC\perp AM \Rightarrow SB \perp (AMN)\Rightarrow SB\perp AN\) (đpcm).
-- Mod Toán 11 HỌC247
-


A. (CDD’C’)
B. (A’B’C’D’)
C. (BDD’B’)
D. (A’BD)
Theo dõi (0) 1 Trả lời -


A. thuộc một mặt phẳng
B. vuông góc với nhau
C. song song với một mặt phẳng
D. song song với nhau
Theo dõi (0) 1 Trả lời -


Mệnh đề nào sau đây là đúng?
bởi Nhat nheo
 25/01/2021
25/01/2021
A. hai đường thẳng phân biệt cùng song song với một mặt phẳng thì song song với nhau.
B. hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.
C. một đường thẳng và một mặt phẳng cùng vuông góc với một mặt phẳng thì song song với nhau.
D. các đường thẳng cùng vuông góc với một đường thẳng thì cùng thuộc một mặt phẳng.
Theo dõi (0) 1 Trả lời -


Đường thẳng a vuông góc với hai đường thẳng phân biệt trong mặt phẳng (P) thì :
bởi Naru to
 24/01/2021
24/01/2021
A. a vuông góc với mặt phẳng (P)
B. a không vuông góc với mặt phẳng (P)
C. a không thể vuông góc với mặt phẳng (P)
D. a có thể vuông góc với mặt phẳng (P)
Theo dõi (0) 1 Trả lời -


Cho hình chóp S.ABCD có ABCD là hình vuông và SA ⊥ (ABCD). Tam giác SOD là:
bởi Phung Hung
 25/01/2021
25/01/2021
A. Tam giác thường
B. Tam giác cân
C. Tam giác đều
D. Tam giác vuông
Theo dõi (0) 1 Trả lời -


Cho hình chóp S.ABCD có ABCD là hình vuông và SA ⊥ (ABCD). Tam giác SBC là tam giác gì?
bởi Thùy Trang
 25/01/2021
25/01/2021
A. Tam giác thường
B. Tam giác cân
C. Tam giác đều
D. Tam giác vuông
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 5 trang 105 SGK Hình học 11
Bài tập 6 trang 105 SGK Hình học 11
Bài tập 8 trang 105 SGK Hình học 11
Bài tập 3.16 trang 145 SBT Hình học 11
Bài tập 3.17 trang 145 SBT Hình học 11
Bài tập 3.18 trang 145 SBT Hình học 11
Bài tập 3.19 trang 145 SBT Hình học 11
Bài tập 3.20 trang 145 SBT Hình học 11
Bài tập 3.21 trang 145 SBT Hình học 11
Bài tập 12 trang 102 SGK Hình học 11 NC
Bài tập 13 trang 102 SGK Hình học 11 NC
Bài tập 14 trang 102 SGK Hình học 11 NC
Bài tập 15 trang 102 SGK Hình học 11 NC
Bài tập 16 trang 103 SGK Hình học 11 NC
Bài tập 17 trang 103 SGK Hình học 11 NC
Bài tập 18 trang 103 SGK Hình học 11 NC






