Giải bài 3.18 tr 145 SBT Hình học 11
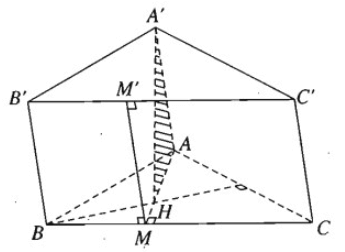
Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi H là trực tâm của tam giác ABC và biết rằng A'H vuông góc với mặt phẳng (ABC). Chứng minh rằng:
a) AA ⊥ BC và AA' ⊥ B'C'.
b) Gọi MM' là giao tuyến của mặt phẳng (AHA') với mặt bên BCC'B', trong đó M ∈ BC và M' ∈ B'C'. Chứng minh rằng tứ giác BCC'B là hình chữ nhật và MM' là đường cao của hình chữ nhật đó.
Hướng dẫn giải chi tiết
a) Ta có BC ⊥ AH và BC ⊥ A'H (vì A'H ⊥ (ABC))
⇒ BC ⊥ (A'HA) ⇒ BC ⊥ AA'
Và B'C' ⊥ AA' (vì BC // B'C')
b) Ta có AA' // BB' // CC' mà BC ⊥ AA' nên tứ giác BCC’B’ là hình chữ nhật. Vì AA' // (BCC'B') nên ta suy ra MM' ⊥ BC và MM' ⊥ B'C' hay MM’ là đường cao của hình chữ nhật BCC’B’.
-- Mod Toán 11 HỌC247
-
Giúp câu 16,17 vs ạ
Theo dõi (0) 0 Trả lời -
Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a ,SA vuông ABCD, SA = a căn 2
bởi Le Nguyen
22/05/2020
a) SA vuông ABCD, SA = a căn 2 a.chứng minh BC vuông (SAB )
b) gọi H là trực tâm tam giác SAB chứng minh BH vuông BC
c) Tính góc giữa đường thẳng SC và mặt phẳng ABCD đ.Gọi M ,N lần lượt là trung điểm SA, SD Chứng minh tam giác HMN là tam giác vuông
Theo dõi (0) 1 Trả lời -
Cho hình chóp SABC có đáy ABC là tam giác vuông tại B cạnh bên SA vuông góc với đáy khẳng định nào sau đây đúng
bởi Ngọc Lan
19/05/2020
Câu 16
Theo dõi (0) 4 Trả lời -
Chứng minh các mặt bên của hình chóp là tam giác vuông?
bởi Quỳnh Chi
16/05/2020
Câu 2 ạ
Theo dõi (0) 1 Trả lời -
Chứng minh BC vuông góc (SAB) biết hình chóp S.ABCD có đáy là ABCD là hình vuông cạnh a
bởi Phương Anh
14/05/2020
Bài 1cho hình chóp SABCD đáy là ABCD là hình vuông cạnh a. SA vuông góc với ABCD và SA= a căn 6.
1)Chứng minh BC vuông góc (SAB),
từ đó suy ra ( SBC) vuông góc ( SAB)?
2)Tính góc giữa đường thẳng SC và mặt phẳng đáy (ABCD)?
Bài 2: Cho tứ giác đều S.ABCD. Gọi M,N lần lượt là trung điểm của SA và SC.
1)AC vuông góc (SBD)
2)(BMN) vuông góc với (SBD)
3)Cho AB=SA=a. Tính góc giữa SA và (ABCD)mọi người giúp mình với ạ mình cảm ơn❤
Theo dõi (0) 1 Trả lời -
Chứng minh rằng AC' vuông góc cới (SBC)?
bởi Anh Duy Nguyễn
08/05/2020
Theo dõi (1) 0 Trả lời
Bài tập SGK khác
Bài tập 3.16 trang 145 SBT Hình học 11
Bài tập 3.17 trang 145 SBT Hình học 11
Bài tập 3.19 trang 145 SBT Hình học 11
Bài tập 3.20 trang 145 SBT Hình học 11
Bài tập 3.21 trang 145 SBT Hình học 11
Bài tập 12 trang 102 SGK Hình học 11 NC
Bài tập 13 trang 102 SGK Hình học 11 NC
Bài tập 14 trang 102 SGK Hình học 11 NC
Bài tập 15 trang 102 SGK Hình học 11 NC
Bài tập 16 trang 103 SGK Hình học 11 NC
Bài tập 17 trang 103 SGK Hình học 11 NC
Bài tập 18 trang 103 SGK Hình học 11 NC
