Bài tập 19 trang 103 SGK Hình học 11 NC

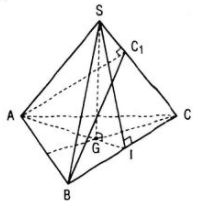
a) Vì SA = SB = SC nên S nằm trên trục của đường tròn ngoại tiếp tam giác ABC.

Mà G là tâm đường tròn ngoại tiếp tam giác ABC nên SG ⊥ mp(ABC)

Gọi I là trung điểm của BC.

Ta có : AI ⊥ BC và BC ⊥ SI

\(\begin{array}{*{20}{l}}
\begin{array}{l}
SI = \sqrt {S{C^2} - I{C^2}} \\
 = \sqrt {{b^2} - \frac{{{a^2}}}{4}}  = \sqrt {\frac{{4{b^2} - {a^2}}}{2}} 
\end{array}\\
{GI = \frac{1}{3}AI = \frac{1}{3}.a\frac{{\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{6}}
\end{array}\)

Trong tam giác vuông SGI ta có :

\(\begin{array}{*{20}{l}}
\begin{array}{l}
SG = \sqrt {S{I^2} - G{I^2}} \\
 = \sqrt {\frac{{4{b^2} - {a^2}}}{4} - \frac{{{a^2}}}{{12}}} 
\end{array}\\
{ = \sqrt {\frac{{12{b^2} - 4{a^2}}}{{12}}}  = \sqrt {\frac{{3{b^2} - {a^2}}}{3}} }
\end{array}\)

b) Kẻ AC₁ ⊥ SC thì (P) chính là mp(ABC₁)

Vì SAC là tam giác cân mà AC1 ⊥ SC nên C₁ nằm giữa S và C khi và chỉ khi 

\(\begin{array}{l}
\widehat {ASC} < {90^0}\\
 \Leftrightarrow A{S^2} + C{S^2} > A{C^2}\\
 \Leftrightarrow 2{b^2} > {a^2}
\end{array}\)

Ta có : AB ⊥ GC và AB ⊥ SG ⇒ AB ⊥ SC

SC ⊥ AC₁ và SC ⊥ AB nên SC ⊥ (ABC₁)

Thể tích tứ diện SABC là:

\(\begin{array}{*{20}{l}}
{{V_{SABC}} = \frac{1}{3}SG.{S_{ABC}} = \frac{1}{3}SC.{S_{AB{C_1}}}}\\
\begin{array}{l}
 \Rightarrow {S_{AB{C_1}}} = \frac{{SG.{S_{ABC}}}}{{SC}}\\
 = \frac{{\sqrt {\frac{{3{b^2} - {a^2}}}{3}} .\frac{{{a^2}\sqrt 3 }}{4}}}{b} = \frac{{{a^2}\sqrt {3{b^2} - {a^2}} }}{{4b}}
\end{array}
\end{array}\)

-- Mod Toán 11 HỌC247