Giải bài 3.19 tr 145 SBT Hình học 11
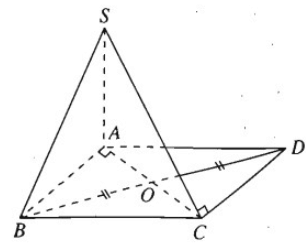
Hình chóp tam giác S.ABC có đáy ABC là tam giác vuông tại A và có cạnh bên SA vuông góc với mặt phẳng đáy là (ABC). Gọi D là điểm đối xứng của điểm B qua trung điểm O của cạnh AC. Chứng minh rằng CD ⊥ CA và CD ⊥ (SCA).
Hướng dẫn giải chi tiết
Ta có SA ⊥ (ABC) ⇒ SA ⊥ DC ⊂ (ABC)
Vì AC và BD cắt nhau tại trung điểm Ocủa mỗi đoạn nên tứ giác ABCD là hình bình hành và ta có AB // CD. Vì AB ⊥ AC nên CD ⊥ CA. Mặt khác ta có CD ⊥ SA, do đó CD⊥(SCA).
-- Mod Toán 11 HỌC247
-
Chứng minh (ADC'B') vuông góc với (ABB'A') trong hình hộp chữ nhật ABCD.A'B'C'D'
bởi Ngọc Diệp
28/04/2020
Theo dõi (0) 1 Trả lời -
Tính giới hạn lim (căn (n^2-n+3)-n)
bởi Đặng Thị Cẩm Như
28/04/2020
Theo dõi (0) 1 Trả lời -
Chứng minh tam giác SAB, SBC là tam giác vuông biết hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh a
bởi 123
22/04/2020
Theo dõi (0) 3 Trả lời -
Chứng minh rằng AB vuông góc với (SIJ) biết hình chóp tứ S.ABCD, đáy là hình chữ nhật, SA=SB
bởi Lê Giang
22/04/2020
cho hình chóp tứ S.ABCD, đáy là hình chữ nhật, SA=SB. Gọi I, J lần lượt là trung điểm của AB và DC . Chứng minh rằng AB vuông góc với (SIJ)
Theo dõi (0) 3 Trả lời -
Chứng minh rằng AB vuông góc với (SIJ) biết hình chóp S.ABCD có đáy là hình chữ nhật SA=SB
bởi Lê Giang
22/04/2020
cho hình chóp tứ S.ABCD, đáy là hình chữ nhật, SA=SB. Gọi I, J lần lượt là trung điểm của AB và DC . Chứng minh rằng AB vuông góc với (SIJ)
Theo dõi (0) 2 Trả lời -
Chứng minh CE vuông góc (SAB) biết hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D
bởi 이민호
20/04/2020
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, AD=CD=a, AB=2a, SA vuông góc (ABCD), E là trung điểm của AB. Chứng minh rằng: CE vuông góc (SAB)Theo dõi (0) 2 Trả lời
Bài tập SGK khác
Bài tập 3.17 trang 145 SBT Hình học 11
Bài tập 3.18 trang 145 SBT Hình học 11
Bài tập 3.20 trang 145 SBT Hình học 11
Bài tập 3.21 trang 145 SBT Hình học 11
Bài tập 12 trang 102 SGK Hình học 11 NC
Bài tập 13 trang 102 SGK Hình học 11 NC
Bài tập 14 trang 102 SGK Hình học 11 NC
Bài tập 15 trang 102 SGK Hình học 11 NC
Bài tập 16 trang 103 SGK Hình học 11 NC
Bài tập 17 trang 103 SGK Hình học 11 NC
Bài tập 18 trang 103 SGK Hình học 11 NC
