Giải bài 6 tr 105 sách GK Toán Hình lớp 11
Cho hình chóp S.ABCD có đáy là hình thoi ABCD và có cạnh SA vuông góc với mặt phẳng (ABCD). Gọi I và K là hai điểm lần lượt lấy trên hai cạnh SB và SD sao cho \(\frac{{SI}}{{SB}} = \frac{{SK}}{{SD}}\). Chứng minh:
a) BD vuông góc với SC;
b) IK vuông góc với mặt phẳng (SAC).
Hướng dẫn giải chi tiết
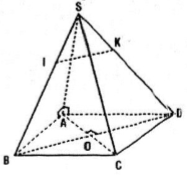
Câu a:
Ta thấy ABCD là hình thoi suy ra các đường chéo AC và BD vuông góc với nhau tại O hay \(BD\perp AC\) (1).
Mặt khác theo giả thiết \(SA\perp (ABCD)\)
\(\Rightarrow BD\perp SA (2)\)
Từ (1) và (2) suy ra \(BD\perp (SAC)\) (3)
\(\Rightarrow BD\perp SC\) (đpcm)
Câu b:
Từ giả thiết \(\frac{SI}{SB}=\frac{SK}{SD}\Rightarrow IK // BD \ (4)\)
Từ (3) và (4) suy ra \(IK\perp (SAC)\) (đpcm)
-- Mod Toán 11 HỌC247
-
Mặt phẳng trung trực của đoạn thẳng AB:
bởi Mai Thuy
25/01/2021
A. luôn vuông góc với AB tại một điểm bất kì trên AB
B. luôn cách đều hai đầu mút A và B
C. luôn vuông góc với AB tại trung điểm của AB
D. luôn song song với AB.
Theo dõi (0) 1 Trả lời -
Cho một điểm S có hình chiếu H trên mặt phẳng (P). Với điểm M bất kì trong (P) ta có:
bởi Nguyễn Ngọc Sơn
25/01/2021
A. SM lớn hơn SH
B. SM không nhỏ hơn SH
C. SM không lớn hơn SH
D. SM nhỏ hơn SH
Theo dõi (0) 1 Trả lời -
Cho tứ diện ABCD có AB = AC = AD; góc BAC bằng góc BAD bằng 600. Gọi M, N là trung điểm của AB và CD. Đường thẳng CD vuông góc với mặt phẳng
bởi Lê Gia Bảo
24/01/2021
A. (ABD)
B. (ABC)
C. (ABN)
D. (CMD)
Theo dõi (0) 1 Trả lời -
Cho hình tứ diện ABCD có ba cạnh AB. BC, CD đôi một vuông góc. Đường vuông góc chung của AB và CD là:
bởi Nguyễn Vân
25/01/2021
A. AC
B. BC
C. AD
D. BD
Theo dõi (0) 1 Trả lời -
Cho hình tứ diện ABCD có ba cạnh AB. BC, CD đôi một vuông góc. Đường thẳng AB vuông góc với :
bởi Mai Linh
25/01/2021
A. (BCD)
B. (ACD)
C. (ABC)
D. (CDI) với I là trung điểm của AB
Theo dõi (0) 1 Trả lời -
Cho hình lập phương ABCD. A’B’C’D’. Hình chiếu vuông góc của A lên mặt phẳng (A’BD) là:
bởi Kim Xuyen
25/01/2021
A. trung điểm của BD
B. trung điểm của A’B
C. trung điểm của A’D
D. tâm O của tam giác BDA’
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 4 trang 105 SGK Hình học 11
Bài tập 5 trang 105 SGK Hình học 11
Bài tập 7 trang 105 SGK Hình học 11
Bài tập 8 trang 105 SGK Hình học 11
Bài tập 3.16 trang 145 SBT Hình học 11
Bài tập 3.17 trang 145 SBT Hình học 11
Bài tập 3.18 trang 145 SBT Hình học 11
Bài tập 3.19 trang 145 SBT Hình học 11
Bài tập 3.20 trang 145 SBT Hình học 11
Bài tập 3.21 trang 145 SBT Hình học 11
Bài tập 12 trang 102 SGK Hình học 11 NC
Bài tập 13 trang 102 SGK Hình học 11 NC
Bài tập 14 trang 102 SGK Hình học 11 NC
Bài tập 15 trang 102 SGK Hình học 11 NC
Bài tập 16 trang 103 SGK Hình học 11 NC
Bài tập 17 trang 103 SGK Hình học 11 NC
Bài tập 18 trang 103 SGK Hình học 11 NC
