Giải bài 3.17 tr 145 SBT Hình học 11
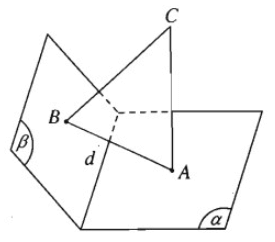
Cho tam giác ABC. Gọi (α) là mặt phẳng vuông góc với đường thẳng CA tại A và (β) là mặt phẳng vuông góc với đường thẳng CB tại B. Chứng minh rằng hai mặt phẳng (α) và (β) cắt nhau và giao tuyến d của chúng vuông góc với mặt phẳng (ABC).
Hướng dẫn giải chi tiết
Hai mặt phẳng (α) và (β) không thể trùng nhau vì nếu chúng trùng nhau thì từ một điểm C ta dựng được hai đường thẳng CA, CB cùng vuông góc với một mặt phẳng, điều đó là vô lí.
Mặt khác (α) và (β) cũng không song song với nhau.
Vì nếu (α) // (β), thì từ CB ⊥ (β) ta suy ra CB ⊥ (α)
Như vậy từ một điểm C ta dựng được hai đường thẳng CA, CB cùng vuông góc với (α), điều đó là vô lí.
Vậy (α) và (β) là hai mặt phẳng không trùng nhau, không song song với nhau và chúng phải cắt nhau theo giao tuyến d, nghĩa là d = (α) ∩ (β)
\(\begin{array}{l}
\left\{ \begin{array}{l}
d \subset \left( \alpha \right)\\
CA \bot \left( \alpha \right)
\end{array} \right. \Rightarrow CA \bot d\,\,\,\left( 1 \right)\\
\left\{ \begin{array}{l}
d \subset \left( \beta \right)\\
CB \bot \left( \beta \right)
\end{array} \right. \Rightarrow CB \bot d\,\,\,\left( 2 \right)
\end{array}\)
Từ (1) và (2) suy ra d ⊥ (ABC).
-- Mod Toán 11 HỌC247
-


Chứng minh SA vuông góc với (ABCD)?
bởi Trần Diệu Ngân
 06/06/2020
06/06/2020
Kiểm tra học kỳ
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tính góc giữa hai đường thẳng (EM, FP)?
bởi Minh Choắt
 05/06/2020
05/06/2020
giúp em giải bài ktra 1 tiết này ạ.
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tính góc giữa đường thẳng SD và mặt phẳng ABCD?
bởi Hàn Thiên Dương
 02/06/2020
02/06/2020
Cho hình chóp s.abcd có đáy là hình vuông cạnh a=3, SA=√3 và SA vuông góc với đáy. Tính góc giữa đường thẳng SD và mặt phẳng ABCD?
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Chứng minh rằng CD vuông góc (SAD)?
bởi Ly Trần Hải
 28/05/2020
28/05/2020
Làm giúp tui câu c vs , mak câu a b cg ko bt đúg ko
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Các đường thẳng đi qua hai đỉnh của hình lập phương ABCD.A'B'C'D' và vuông góc cới đường thẳng AC là?
bởi Hồ Lô
 28/05/2020
28/05/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Cho hình chóp S.ABCD có ABCD là hình vuông cạnh a tâm O, SA vuông góc (ABCD), SA=2aa.Tính góc giữa đt SB và mp SAC
bởi Lâm Oanh
 23/05/2020
Theo dõi (0) 0 Trả lời
23/05/2020
Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 8 trang 105 SGK Hình học 11
Bài tập 3.16 trang 145 SBT Hình học 11
Bài tập 3.18 trang 145 SBT Hình học 11
Bài tập 3.19 trang 145 SBT Hình học 11
Bài tập 3.20 trang 145 SBT Hình học 11
Bài tập 3.21 trang 145 SBT Hình học 11
Bài tập 12 trang 102 SGK Hình học 11 NC
Bài tập 13 trang 102 SGK Hình học 11 NC
Bài tập 14 trang 102 SGK Hình học 11 NC
Bài tập 15 trang 102 SGK Hình học 11 NC
Bài tập 16 trang 103 SGK Hình học 11 NC
Bài tập 17 trang 103 SGK Hình học 11 NC
Bài tập 18 trang 103 SGK Hình học 11 NC