Bài tập 1 trang 41 SGK Đại số 10

Lý thuyết10 Trắc nghiệm

21 BT SGK

111 FAQ

Giải bài 1 tr 41 sách GK Toán ĐS lớp 10

Vẽ đồ thị hàm số:

a) $y = 2x - 3$;

b) $y = \sqrt{2}$;

c) $y=-\frac{3x}{2}+7;$

d) $y = |x|-1$.

Toán 10 Chương 2 Bài 2 Trắc nghiệm Toán 10 Chương 2 Bài 2 Giải bài tập Toán 10 Chương 2 Bài 2

Hướng dẫn giải chi tiết bài 1

Câu a:

Đồ thị hàm số y = 2x - 3 là đường thẳng đi qua hai điểm $A(0; - 3), B(\frac{3}{2};0).$

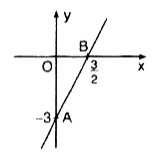
Câu b:

Đồ thị là đường thẳng song song với Ox và cắt trục tung tại điểm $M(0;\sqrt{2})$

Câu c:

Đồ thị là đường thẳng đi qua hai điểm A(0;7), B(2;4)

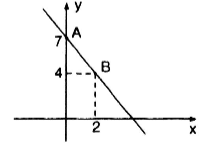
Câu d:

$y = |x| - 1 =\left\{\begin{matrix} -x-1 \ voi \ x<0\\ x-1 \ voi \ x\geq 0 \end{matrix}\right.$

Đồ thị là hai nửa đường thẳng cùng xuất phát từ điểm có toạ độ (0;-1) đối xứng với nhau qua trục Oy.

-- Mod Toán 10 HỌC247

Nếu bạn thấy hướng dẫn giải Bài tập 1 trang 41 SGK Đại số 10 HAY thì click chia sẻ

Toạ độ đỉnh của hàm số y=x²-2x-3 là?

bởi Liêu Phát Lợi 24/01/2022

Giúp với nhanh nhanh lên nha

Theo dõi (0) 1 Trả lời
Tìm giá trị thực của tham số m để phương trình | x | + 1 = x 2 + m có nghiệm duy nhất.

bởi Nguyễn Quốc Ca 24/11/2021

Tìm giá trị thực của tham số $m$ để phương trình $| x | + 1 = x^{2} + m$ có nghiệm duy nhất.

Theo dõi (0) 0 Trả lời
Tìm tọa độ đỉnh, trục đối xứng và lập bảng biến thiên các hàm số sau: (y = x^2 - 3x + 2)

bởi Ŋgọç Dĭệu 18/11/2021

Tìm tọa độ đỉnh, trục đối xứng và lập bảng biến thiên các hàm số sau

y = x² - 3x + 2

y = -2x² + 4x

Theo dõi (0) 0 Trả lời
Vẽ đồ thị của các hàm số sau: y= 3x-5

bởi ánh nhật 01/11/2021

Câu 1:Vẽ đồ thị của các hàm số sau: a) y= 3x-5 ; b) y= 5x-3

Theo dõi (0) 1 Trả lời
Tìm giao điểm của đường thẳng y = 5x + 4 với y = 5x-11

bởi Hồ Quý 27/10/2021

1. Tìm hàm số y=f(x) biết đồ thị hàm số của nó là đường thẳng A(3;4) và vuông góc với đường thẳng y = 1/3.x+5

2. Tìm giao điểm của đường thẳng y = 5x + 4 với y = 5x-11

3. Tìm các hệ số a, b của đường thẳng y=3(x-4)-3

4. Tìm giao điểm của đường thẳng y = 4x + 3 với trục tung.

5. Tìm a để đường thẳng y=ax+3 qua A(5;-5)

6. Tìm hệ số góc của đường thẳng qua A(2;5) B(-4;2)

Theo dõi (0) 0 Trả lời
Cho hàm số y=|3-2x|. Tìm GTLN, GTNN của hàm số trên [0;1] dựa vào đồ thị hàm số.

bởi Nhạt Cần Mắm 25/10/2021

Cho hàm số y=|3-2x|. Tìm GTLN, GTNN của hàm số trên [0;1] dựa vào đồ thị hàm số

Theo dõi (0) 0 Trả lời