Bài tập 25 trang 54 SGK Toán 10 NC
Đi một hãng taxi quy định giá thuê xe đi mỗi kilômét là 6 nghìn đồng đối 10 km đầu tiên và 2,5 nghìn đồng đối với các kilômét tiếp theo. Một khách thuê taxi đi quãng đường x kilômét phải trả số tiền là y nghìn đồng. Khi đó, y là một hàm số của đối số x, xác định với mọi x ≥ 0.
a) Hãy biểu diễn y như một hàm số bậc nhất trên từng khoảng ứng với đoạn [0;10] và khoảng (10;+∞)
b) Tính \(f(8), f(10)\) và \(f(18)\).
c) Vẽ đồ thị của hàm số \(y = f(x)\) và lập bảng biến thiên cùa nó.
Hướng dẫn giải chi tiết
a) Ta có
Nếu \(x \in \left[ {0;10} \right]\) tức hành khách đi không quá 10km thì số tiền phải trả là: y = 6x (nghìn đồng)
Nếu \(x \in \left( {10; + \infty } \right)\) tức hành khách đi hơn 10km thì số tiền phải trả là:
\(y=10.6+(x-10).2,5\) (nghìn đồng) \(\Leftrightarrow y = 2,5x + 35\)
Vậy \(y = \left\{ \begin{array}{l}
6x,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,0 \le x \le 10\\
2,5x + 35,\,\,\,x > 10
\end{array} \right.\)
b) Ta có:
\(\begin{array}{l}
f\left( 8 \right) = 48\\
f\left( {10} \right) = 60\\
f\left( {18} \right) = 80
\end{array}\)
c) Bảng giá trị
Bảng biến thiên

Đồ thị hàm số
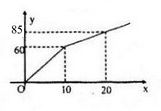
-- Mod Toán 10 HỌC247
-


Viết phương trình hàm số y = ax + b của đường thẳng:
a) Đi qua điểm A(4; 3), B(2;- 1).
b) Đi qua điểm A(1;- 1) và song song với Ox.
Theo dõi (0) 2 Trả lời -


cho hàm số bậc nhất : y = f(x) = (m -1)x +2m +1 (dm).
- Khảo sát và vẽ đồ thị hàm số khi m = 2.
- Tìm m để đồ thị hàm số (dm) đi qua điểm A(4, -1).
- Tìm m để hàm số nghịch biến trên tập xác định.
- Tìm điểm cố định của đồ thị hàm số (dm) đi qua.
Theo dõi (0) 3 Trả lời -


Hãy viết phương trình hàm số bậc nhất đường thẳng (d) : y = ax + b
a) Đi qua 2 điểm A(4; 3) và B(2; -1)
b) Đi qua điểm A(1; -1) và song trục ox.
Theo dõi (0) 2 Trả lời




.PNG)



