Giải bài 2.12 tr 35 SBT Đại số 10
Xác định các hệ số a và b để đồ thị của hàm số y = ax+b đi qua các điểm sau
a) \(A\left( {\frac{2}{3}; - 2} \right)\) và B(0;1)
b) M(−1;−2) và N(99;−2)
c) P(4;2) và Q(1;1)
Hướng dẫn giải chi tiết
a) Vì đồ thị đi qua \(A\left( {\frac{2}{3}; - 2} \right)\) nên ta có phương trình \(a.\frac{2}{3} + b = - 2\).
Tương tự, dựa vào tọa độ của B(0;1) ta có 0+b = 1
Vậy, ta có hệ phương trình.
\(\left\{ \begin{array}{l}
a.\frac{2}{3} + b = - 2\\
b = 1
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
a = - \frac{9}{2}\\
b = 1
\end{array} \right.\)
Vậy \(a = - \frac{9}{2}, b =1\)
b) Vì đồ thị đi qua M(−1;−2) nên ta có phương trình a.(−1)+b = −2.
Tương tự, dựa vào tọa độ của N(99;−2) ta có 99a+b = −2
Vậy, ta có hệ phương trình.
\(\left\{ \begin{array}{l}
- a + b = - 2\\
99a + b = - 2
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
a = 0\\
b = - 2
\end{array} \right.\)
Vậy a = 0; b = −2.
c) Vì đồ thị đi qua P(4;2) nên ta có phương trình 4a+b = 2.
Tương tự, dựa vào tọa độ của Q(1;1) ta có a+b = 1
Vậy, ta có hệ phương trình.
\(\left\{ \begin{array}{l}
4a + b = 2\\
a + b = 1
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
a = \frac{1}{3}\\
b = \frac{2}{3}
\end{array} \right.\)
Vậy \(a=\frac{1}{3}, b=\frac{2}{3}\)
-- Mod Toán 10 HỌC247
-


Tìm giá trị của tham số m để đường thẳng y = m cắt đồ thị hàm số y = 2x^2+ 2x-3?
bởi Hoàng Lan
 23/06/2020
23/06/2020
Tìm giá trị của tham số m để đường thẳng y = m cắt đồ thị hàm số y = 2x^2+ 2x-3?
Theo dõi (0) 2 Trả lời -


Bảng xét dấu của biểu thức f (x) =x -1
bởi An Nhiên
 03/06/2020
03/06/2020
 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Đồ thị ở hình bên là đồ thị hàm số nào dưới đây?
bởi Trịnh Lan Trinh
 25/05/2020
25/05/2020
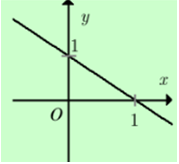
A. y = x + 1.
B. y = -x + 2.
C. y = 2x + 1.
D. y = -x + 1.
Theo dõi (0) 1 Trả lời -


Đỉnh của parabol (P): y = 3\({x^2}\) – 2x + 1 là:
bởi Nguyễn Lệ Diễm
 25/05/2020
Theo dõi (0) 1 Trả lời
25/05/2020
Theo dõi (0) 1 Trả lời -


Trong các hàm số sau, hàm số nào có đồ thị nhận đường thẳng x = 1 làm trục đối xứng?
bởi Nguyễn Thanh Trà
 25/05/2020
25/05/2020
A. y = -2x2 + 4x + 1.
B. y = 2x2 + 4x – 3.
C. y = 2x2 - 2x – 1.
D. y = x2– x + 2.
Theo dõi (0) 1 Trả lời -

 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 2.10 trang 35 SBT Toán 10
Bài tập 2.11 trang 35 SBT Toán 10
Bài tập 2.13 trang 35 SBT Toán 10
Bài tập 2.15 trang 36 SBT Hình 10
Bài tập 2.16 trang 36 SBT Toán 10
Bài tập 2.17 trang 36 SBT Toán 10
Bài tập 17 trang 51 SGK Toán 10 NC
Bài tập 18 trang 52 SGK Toán 10 NC
Bài tập 19 trang 52 SGK Toán 10 NC
Bài tập 20 trang 53 SGK Toán 10 NC
Bài tập 21 trang 53 SGK Toán 10 NC
Bài tập 22 trang 53 SGK Toán 10 NC
Bài tập 23 trang 53 SGK Toán 10 NC
Bài tập 24 trang 53 SGK Toán 10 NC





