Câu hỏi (25 câu):
-
Câu 1: Mã câu hỏi: 75407
Tính \(I = \int\limits_0^1 {{{\rm{e}}^{3x}}.{\rm{d}}x} \)
- A. \(I = {{\rm{e}}^3} - 1\)
- B. \(I=e-1\)
- C. \(I = \frac{{{{\rm{e}}^3} - 1}}{3}\)
- D. \(I = {{\rm{e}}^3} + \frac{1}{2}\)
-
Câu 2: Mã câu hỏi: 75408
Họ nguyên hàm của hàm số \(f\left( x \right) = 2x + \sin 2x\) là
- A. \({x^2} + 2\cos 2x + C\)
- B. \({x^2} + \frac{1}{2}\cos 2x + C\)
- C. \({x^2} - \frac{1}{2}\cos 2x + C\)
- D. \({x^2} - 2\cos 2x + C\)
-
Câu 3: Mã câu hỏi: 75410
Cho hàm số \(f(x)\) có đạo hàm liên tục trên đoạn [1;3] thỏa mãn \(f(1)=2\) và \(f(3)=9\). Tính \(I = \int\limits_1^3 {f'\left( x \right){\rm{d}}x} \).
- A. I = 11
- B. I = 7
- C. I = 2
- D. I = 18
-
Câu 4: Mã câu hỏi: 75412
Cho hai hàm số \(f(x)\) và \(g(x)\) liên tục trên K, \(a,\,\,b \in K\). Khẳng định nào sau đây là khẳng định sai?
- A. \(\int\limits_a^b {kf\left( x \right){\rm{d}}x} = k\int\limits_a^b {f\left( x \right){\rm{d}}x} \)
- B. \(\int\limits_a^b {f\left( x \right)g\left( x \right){\rm{d}}x} = \int\limits_a^b {f\left( x \right){\rm{d}}x} .\int\limits_a^b {g\left( x \right){\rm{d}}x} \)
- C. \(\int\limits_a^b {\left[ {f\left( x \right) + g\left( x \right)} \right]{\rm{d}}x} = \int\limits_a^b {f\left( x \right){\rm{d}}x} + \int\limits_a^b {g\left( x \right){\rm{d}}x} \)
- D. \(\int\limits_a^b {\left[ {f\left( x \right) - g\left( x \right)} \right]{\rm{d}}x} = \int\limits_a^b {f\left( x \right){\rm{d}}x} - \int\limits_a^b {g\left( x \right){\rm{d}}x} \)
-
Câu 5: Mã câu hỏi: 75413
Cho tích phân \(I = \int\limits_1^{\rm{e}} {\frac{{\ln x}}{x}\,{\rm{d}}x} \). Nếu đặt \(t = \ln x\) thì
- A. \(I = \int\limits_0^{\rm{1}} {\frac{t}{{{{\rm{e}}^t}}}\,{\rm{d}}t} \)
- B. \(I = \int\limits_0^1 {{t^2}\,{\rm{d}}t} \)
- C. \(I = \int\limits_0^{\rm{1}} {t\,{\rm{d}}t} \)
- D. \(I = \int\limits_1^{\rm{e}} {t\,{\rm{d}}t} \)
-
Câu 6: Mã câu hỏi: 75414
Diện tích S của hình phẳng giới hạn bởi đồ thị hàm số \(y=x^2\), trục hoành Ox, các đường thẳng \(x=1, x=2\) là
- A. \(S = \frac{8}{3}\)
- B. \(S = \frac{7}{3}\)
- C. S = 8
- D. S = 7
-
Câu 7: Mã câu hỏi: 75416
Cho hàm số \(f\left( x \right) = \cos x\). Mệnh đề nào sau đây đúng
- A. \(\int {f\left( x \right){\rm{d}}x = - \sin x + C} \)
- B. \(\int {f\left( x \right){\rm{d}}x = - \cos x + C} \)
- C. \(\int {f\left( x \right){\rm{d}}x = \cos x + C} \)
- D. \(\int {f\left( x \right){\rm{d}}x = \sin x + C} \)
-
Câu 8: Mã câu hỏi: 75419
Cho hàm \(y=f(x)\) liên tục và không âm trên [a;b]. Tính thể tích khối tròn xoay được tạo thành khi quay hình phẳng (H) được giới hạn bởi các đường \(y=f(x)\), trục Ox và hai đường thẳng \(x=a, x=b (a<b)\) xung quanh trục Ox.
- A. \(\int\limits_a^b {{f^2}\left( x \right)\,{\rm{d}}x} \,\)
- B. \(2\pi \int\limits_a^b {{f^2}\left( x \right)\,{\rm{d}}x} \,\)
- C. \(\pi \int\limits_a^b {{f^2}\left( x \right)\,{\rm{d}}x} \,\)
- D. \(\pi \int\limits_a^b {{f}\left( x \right)\,{\rm{d}}x} \,\)
-
Câu 9: Mã câu hỏi: 75422
Cho \(I = \int {\left( {{x^2} + 1} \right)2xdx} \). Bằng cách đặt \(t=x^2+1\), khẳng định nào sau đây đúng
- A. \(I = 2\int {tdt} \)
- B. \(I = \frac{1}{2}\int {tdt} \)
- C. \(I = \int {\left( {t + 1} \right)dt} \)
- D. \(I = \int {tdt} \)
-
Câu 10: Mã câu hỏi: 75426
Cho hàm số \(f(x)\) liên tục trên [a;b]. Hãy chọn mệnh đề sai dưới đây:
- A. \(\int\limits_a^b {f\left( x \right){\rm{d}}x} = \int\limits_b^a {f\left( x \right){\rm{d}}x} \)
- B. \(\int\limits_a^b {f\left( x \right){\rm{d}}x} = \int\limits_a^c {f\left( x \right){\rm{d}}x} + \int\limits_c^b {f\left( x \right){\rm{d}}x} \) với \(c \in \left[ {a;b} \right]\)
- C. \(\int\limits_a^b {k{\rm{d}}x} = k\left( {b - a} \right)\), \(\forall k \in R\)
- D. \(\int\limits_a^b {f\left( x \right){\rm{d}}x} = - \int\limits_b^a {f\left( x \right){\rm{d}}x} \)
-
Câu 11: Mã câu hỏi: 75428
Tính tích phân \(I = \int\limits_0^{\rm{\pi }} {x\cos x{\rm{d}}x} \) bằng cách đặt \(\left\{ \begin{array}{l}
u = x\\
{\rm{d}}v = \cos x{\rm{d}}x
\end{array} \right.\). Mệnh đề nào dưới đây đúng?- A. \(I = x\sin x\left| {{}_0^{\rm{\pi }}} \right. + \int\limits_0^{\rm{\pi }} {\sin x{\rm{d}}x} \)
- B. \(I = x\sin x\left| {{}_0^{\rm{\pi }}} \right. - \int\limits_0^{\rm{\pi }} {\sin x{\rm{d}}x} \)
- C. \(I = x\sin x\left| {{}_0^{\rm{\pi }}} \right. - \int\limits_0^{\rm{\pi }} {\cos x{\rm{d}}x} \)
- D. \(I = x\cos x\left| {{}_0^{\rm{\pi }}} \right. - \int\limits_0^{\rm{\pi }} {\sin x{\rm{d}}x} \)
-
Câu 12: Mã câu hỏi: 75430
Giả sử hàm số \(y=f(x)\) liên tục trên R và \(\int\limits_3^5 {f\left( x \right){\rm{d}}x = a} \), \(\left( {a \in R} \right)\). Tích phân \(I = \int\limits_1^2 {f\left( {2x + 1} \right){\rm{d}}x} \) có giá trị là
- A. \(I = \frac{1}{2}a + 1\)
- B. \(I=2a+1\)
- C. \(I=2a\)
- D. \(I = \frac{1}{2}a\)
-
Câu 13: Mã câu hỏi: 75431
Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số \(y=e^x\), trục Ox và hai đường thẳng \(x=0, x=1\). Thể tích của khối tròn xoay tạo thành khi quay (H) xung quanh trục Ox là
- A. \(\frac{\pi }{2}\left( {{e^2} - 1} \right)\)
- B. \(\pi \left( {{e^2} + 1} \right)\)
- C. \(\frac{\pi }{2}\left( {{e^2} + 1} \right)\)
- D. \(\pi \left( {{e^2} - 1} \right)\)
-
Câu 14: Mã câu hỏi: 75432
Viết công thức tính diện tích hình phẳng được giới hạn bởi đồ thị hàm số \(y=f(x)\), trục Ox và các đường thẳng \(x = a,x = b\,\,\left( {a < b} \right).\)
- A. \(\int\limits_a^b {\left| {f\left( x \right)} \right|dx} \)
- B. \(\pi \int\limits_a^b {f\left( x \right)dx} \)
- C. \(\int\limits_a^b {{f^2}\left( x \right)dx} \)
- D. \(\int\limits_a^b {f\left( x \right)dx} \)
-
Câu 15: Mã câu hỏi: 75433
Kết quả của \(I = \int {x{e^x}} {\rm{d}}x\) là
- A. \((I = {e^x} + x{e^x} + C\)
- B. \(I = x{e^x} - {e^x} + C\)
- C. \(I = \frac{{{x^2}}}{2}{e^x} + C\)
- D. \(I = \frac{{{x^2}}}{2}{e^x} + {e^x} + C\)
-
Câu 16: Mã câu hỏi: 75434
Một xe mô tô đang chạy với vận tốc 20 m/s thì người lái xe nhìn thấy một chướng ngại vật nên đạp phanh. Từ thời điểm đó, mô tô chuyển động chậm dần với vận tốc \(v\left( t \right) = 20 - 5t\), trong đó t là thời gian (được tính bằng giây) kể từ lúc đạp phanh. Quãng đường mà mô tô đi được từ khi người lái xe đạp phanh cho đến lúc mô tô dừng lại là
- A. 40 m
- B. 80 m
- C. 60 m
- D. 20 m
-
Câu 17: Mã câu hỏi: 75436
Biết \(I = \int\limits_1^{\rm{e}} {\frac{{\ln x}}{{x\left( {\ln x + 2} \right)}}{\rm{d}}x = a\ln \frac{3}{2} + b,\,\,\left( {a,b \in Q} \right)} \). Mệnh đề nào sau đây đúng?
- A. \(a-b=1\)
- B. \(2a+b=1\)
- C. \(a+2b=0\)
- D. \({a^2} + {b^2} = 4\)
-
Câu 18: Mã câu hỏi: 75438
Gọi \(F(x)\) là một nguyên hàm của hàm số \(f\left( x \right) = x{{\rm{e}}^{ - x}}\). Tính \(F(x)\) biết \(F(0)=1\).
- A. \(F\left( x \right) = \left( {x + 1} \right){{\rm{e}}^{ - x}} + 2\)
- B. \(F\left( x \right) = - \left( {x + 1} \right){{\rm{e}}^{ - x}} + 2\)
- C. \(F\left( x \right) = - \left( {x + 1} \right){{\rm{e}}^{ - x}} + 1\)
- D. \(F\left( x \right) = \left( {x + 1} \right){{\rm{e}}^{ - x}} + 1\)
-
Câu 19: Mã câu hỏi: 75440
Biết \(F(x)\) là một nguyên hàm của \(f\left( x \right) = \frac{1}{{x + 1}}\) và \(F(0)=2\) thì \(F(1)\) bằng.
- A. \(\ln 2\)
- B. 3
- C. 4
- D. \(2+\ln 2\)
-
Câu 20: Mã câu hỏi: 75441
Giả sử \(\int\limits_1^2 {\frac{1}{{2x + 1}}{\rm{d}}x} = \ln \sqrt {\frac{a}{b}} \) với \(a,b \in N*\) và \(\frac{a}{b}\) tối giản. Tính \(M = {a^2} + {b^2}\).
- A. M = 28
- B. M = 34
- C. M = 14
- D. M = 8
-
Câu 21: Mã câu hỏi: 75442
Tính diện tích S của hình phẳng giới hạn bởi hai đồ thị hàm số \(y=2x^2\) và \(y=5x-2\).
-
Câu 22: Mã câu hỏi: 75443
Biết \(F(x)\) là một nguyên hàm của hàm \(f\left( x \right) = x\ln \left( {x + 1} \right)\) và \(F\left( 0 \right) = 0,F\left( 2 \right) = a\ln b\) với \(a,b \in Q\). Tính \(P=a+b\)
-
Câu 23: Mã câu hỏi: 75444
Cho hàm số \(f(x)\) có đạo hàm liên tục trên đoạn [0;1[ và thỏa mãn \(f\left( 0 \right) = 6,\int\limits_0^1 {\left( {2x - 2} \right).f'\left( x \right){\rm{d}}x = 6} \). Tích phân \(\int_0^1 {f\left( x \right){\rm{d}}x} \).
-
Câu 24: Mã câu hỏi: 75445
Cho hàm số \(y=f(x)\) có đạo hàm liên tục trên [- 2;4]. Đồ thị của hàm số \(y=f'(x)\) được cho như hình bên. Diện tích hình phẳng giới hạn bởi trục Ox và đồ thị hàm số \(y=f'(x)\) trên đoạn [-2;1] và [1;4] lần lượt bằng 9 và 12. Cho \(f(1)=3\). Tính tổng \(f\left( { - 2} \right) + f\left( 4 \right).\)
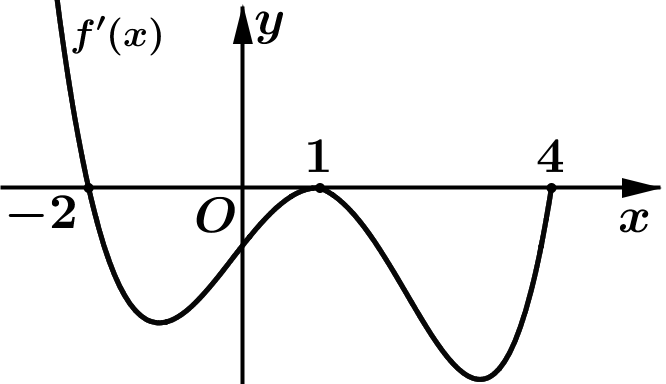
-
Câu 25: Mã câu hỏi: 75446
Cho hàm số \(f(x)\) thỏa mãn \(f\left( 2 \right) = - \frac{1}{5},f'\left( x \right) = {x^3}{\left[ {f\left( x \right)} \right]^2}\) và \(f\left( x \right) \ne 0\) với mọi \(x \in R\). Tính giá trị của \(f(1)\)






