Hôm nay chúng ta tiếp tục học bài 5: Tổng hợp hai dao động điều hòa cùng phương, cùng tần số. Phương pháp Fre-Nen, đây là bài cuối cùng của chương Dao động điều hòa
Tổng hợp dao động là nói gọn, nói chính xác đó là tổng hợp hai dao động điều hòa cùng phương, cùng tần số. Để hiểu cụ thể và chi tiết hơn, mời các em cùng nghiên cứu nội dung của bài nhé.
Tóm tắt lý thuyết
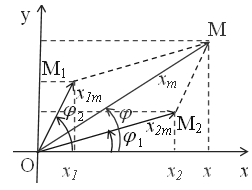
2.1. Vectơ quay
- Ta có thể biểu diễn một dao động \(x = A\cos (\omega t + \varphi )\) bằng một vectơ quay \(\overrightarrow{OM}\) tại thời điểm ban đầu có các đặc điểm sau:
+ Có góc tai góc tọa độ của Ox
+ Có độ dài bằng biên độ dao động; OM = A.
+ Hợp với Ox một góc \(\small \varphi\)
- Hay: \(\overrightarrow{OM} \left\{\begin{matrix} |\overrightarrow{OM}| = A \ \ \ \ \\ (\overrightarrow{OM},\Delta ) = \varphi \end{matrix}\right.\)
2.2. Phương pháp giản đồ Fre-nen
a. Đặt vấn đề
- Tìm tổng của hai dao động
\(\left\{\begin{matrix} x_1 = A_1 \cos (\omega t + \varphi _1)\\ x_2 = A_2 \cos (\omega t + \varphi _2) \end{matrix}\right.\)
b. Phương pháp giản đồ Fre-nen
- Ta lần lượt ta vẽ hai vec tơ quay đặt trưng cho hai dao động:
- Ta thấy \(\small \underset{OM_1}{\rightarrow}\) và \(\small \underset{OM_2}{\rightarrow}\) quay với tốc độ góc ω thì \(\small \underset{OM}{\rightarrow}\) cũng quay với tốc độ góc là ω.
- Phương trình tổng hợp
\(x = A\cos (\omega t + \varphi )\)
\(\small \Rightarrow\) Kết luận: Dao động tổng hợp của hai dao động điều hòa cùng phương, cùng tần số là một dao động điều hòa cùng phương, cùng tần số với hai dao động đó.
- Trong đó:
\(A = \sqrt{A_{1}^{2} + A_{2}^{2} + 2A_1A_2\cos (\varphi _2 - \varphi _1)}\) (1)
\(\tan \varphi = \frac{A_1 \sin \varphi _1 + A_2 \sin \varphi _2}{A_1 \cos \varphi _1 + A_2 \cos \varphi _2}\) (2)
c. Ảnh hưởng của độ lệch pha
\(\ \Delta \varphi = \varphi _2 - \varphi _1 = k2 \pi\): x1, x2 cùng pha \(\Rightarrow \left\{\begin{matrix} A = A_1 + A_2\\ \varphi = \varphi _1 = \varphi _2 \end{matrix}\right.\)
\(\ \Delta \varphi = \varphi _2 - \varphi _1 = (2k + 1) \pi\): x1, x2 ngược pha \(\Rightarrow \left\{\begin{matrix} A = |A_1 - A_2| \ \ \ \ \ \ \ \ \\ \varphi = \varphi _1 \ neu\ A_1 > A_2 \end{matrix}\right.\)
\(\ \Delta \varphi = (2k + 1) \frac{\pi}{2} \Rightarrow x_1 \perp x_2 \Rightarrow A = \sqrt{A_{1}^{2} + A_{2}^{2}}\)
Bài tập minh họa
Bài 1:
Tổng hợp các dao động sau:
\(\\ a/ \left\{\begin{matrix} x_1 = 2 \cos (2 \pi t - \pi )\\ x_2 = 3 \cos (2 \pi t + \pi ) \end{matrix}\right. \\ b/ \left\{\begin{matrix} x_1 = 5 \cos ( \pi t - \frac{\pi }{3})\\ x_2 = \cos ( \pi t + \frac{2\pi }{3}) \end{matrix}\right. \\ c/ \left\{\begin{matrix} x_1 =6 \cos 4 \pi t \ \ \ \ \ \ \ \\ x_2 = 6 \cos (4 \pi t + \frac{\pi }{3}) \end{matrix}\right. \\ d/ \left\{\begin{matrix} x_1 = 4 \cos (5 \pi t + \frac{\pi }{6}) \ \ \ \ \\ x_2 = 4\sqrt{3} \cos (5 \pi t - \frac{\pi }{3}) \end{matrix}\right.\)
Hướng dẫn giải:
a/ \(\Delta \varphi = \pi - (- \pi) = 2 \pi\): x1, x2 cùng pha
\(\Rightarrow \left\{\begin{matrix} A = A_1 + A_2 = 2 + 3 = 5 \ cm\\ \varphi = \pi ;\ \varphi =- \pi \hspace{2,3cm} \end{matrix}\right.\)
\(\rightarrow x = 5\cos (2 \pi t \pm \pi )\ (cm)\)
b/ \(\Delta \varphi = \frac{2 \pi}{3} - \frac{\pi }{3} = \pi\): x1, x2 ngược pha
\(\Rightarrow \left\{\begin{matrix} A = |A_1 - A_2| = |5-1| = 4 \ cm\\ \varphi = \varphi _1 = -\frac{\pi }{3}\ (Vi\ A_1 > A_2) \ \ \ \ \end{matrix}\right.\)
\(\rightarrow x = 4 \cos (\pi t - \frac{\pi}{3}) \ (cm)\)
c/ \(\left\{\begin{matrix} x_1 = 6 \cos 4 \pi t \ (cm) \ \ \ \ \ \ \ \rightarrow \left\{\begin{matrix} A_1 = 6 \ cm\\ \varphi _1 = 0 \ \ \ \ \end{matrix}\right.\\ x_2 = 6 \cos (4 \pi t + \frac{\pi}{3}) \ (cm) \rightarrow \left\{\begin{matrix} A_2 = 6\ cm\\ \varphi _2 = \frac{\pi }{3} \ \ \ \ \end{matrix}\right. \end{matrix}\right.\)
\(\cdot \ A = \sqrt{6^2 + 6^2 + 2.6.6 \cos \frac{\pi}{3}} = 6\sqrt{3}\ cm\)
\(\cdot \ \tan \varphi = \frac{6.\sin 0 + 6. \sin \frac{\pi }{3}}{6. \cos 0 + 6.\cos \frac{\pi }{3}} = \frac{3\sqrt{3}}{9} = \frac{\sqrt{3}}{3} \Rightarrow \varphi = \frac{\pi }{6}\)
d/ \(\left\{\begin{matrix} x_1 = 4\cos (4\pi t + \frac{\pi}{6})\ (cm)\ \ \ \ \\ x_2 = 4\sqrt{3} \cos (5 \pi t - \frac{\pi }{3})\ (cm) \end{matrix}\right.\)
\(\Delta \varphi = \frac{\pi }{2} - \left ( - \frac{\pi}{3} \right ) = \frac{\pi }{2}\)
\(A = \sqrt{A_{1}^{2} + A_{2}^{2}} = 8 \ (cm)\)
\(\tan \varphi = \frac{4 \sin \frac{\pi}{6} + 4\sqrt{3} \sin -\left ( - \frac{\pi}{3} \right )}{4 \cos \frac{\pi}{6} + 4\sqrt{3} \cos -\left ( - \frac{\pi}{3} \right )} = \frac{-4}{4\sqrt{3}}\)
\(\rightarrow \tan \varphi = -\frac{1}{\sqrt{3}} \Rightarrow \varphi = -\frac{\pi }{6}\)
\(\rightarrow x = 8\cos (5 \pi t - \frac{\pi }{6})\ (cm)\)
Bài 2:
Cho 2 dao động cùng phương, cùng tần số có phương trình \(\left\{\begin{matrix} x_1 = A_1 \cos (\omega t + \frac{\pi }{3})\ (cm)\\ x_2 = A_2 \cos (\omega t - \frac{\pi }{2})\ (cm) \end{matrix}\right.\)
Dao động tổng hợp \(x = x_1 + x_2 = 6\sqrt{3}\cos (\omega t + \varphi )\). Tìm giá trị lớn nhất của \(A_2\) khi thay đổi \(A_1\)?
Hướng dẫn giải:
Định lý sin: \(\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}\)
\(x=x_1 + x_2 \Rightarrow \overrightarrow{A} = \overrightarrow{A_1} + \overrightarrow{A_2}\)
Ta có: \(\frac{A_2}{\sin \alpha } = \frac{A}{\sin \frac{\pi }{6}} \Rightarrow A_2 = \frac{A}{\sin \frac{\pi }{6}}. \sin \alpha\)
\(\Rightarrow A_2 = \frac{6\sqrt{3}}{\frac{1}{2}}.\sin \alpha = 12\sqrt{3}.\sin \alpha\)
4. Luyện tập Bài 5 Vật lý 12
Qua bài giảng Tổng hợp hai dao động điều hòa và Phương pháp Fre-Nen này, các em cần hoàn thành 1 số mục tiêu mà bài đưa ra như :
- Biểu diễn được phương trình dao động điều hòa bằng phương pháp vectơ quay.
- Vận dụng được phương pháp giản đồ Fre – nen để tìm phương trình dao động tổng hợp hai dao động điều hòa cùng phương, cùng tần số.
4.1. Trắc nghiệm
Các em có thể hệ thống lại nội dung kiến thức đã học được thông qua bài kiểm tra Trắc nghiệm Vật lý 12 Bài 5 cực hay có đáp án và lời giải chi tiết.
-
- A. \(x = 5\sqrt 2 cos\left( {2\pi t + \frac{\pi }{2}} \right)\,\,cm\)
- B. \(x = 5\sqrt 2 cos\left( {2\pi t} \right)\,\,cm\)
- C. \(x = 5\sqrt 2 cos\left( {2\pi t - \frac{\pi }{2}} \right)\,\,cm\)
- D. \(x = 5\sqrt 2 cos\left( {2\pi t + \frac{\pi }{6}} \right)\,\,cm\)
-
- A. \(x= 7,9 cos(5 \pi t + \frac{41\pi}{180})\)
- B. \(x= 7,9 cos( \pi t + \frac{41\pi}{180})\)
- C. \(x= 7,9 cos(5 \pi t - \frac{41\pi}{180})\)
- D. \(x= 7,9 cos( \pi t - \frac{41\pi}{180})\)
-
- A. 81 cm/s
- B. 81,7 cm/s
- C. 81,7 m/s
- D. 81 m/s
Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức về bài học này nhé!
4.2. Bài tập SGK và Nâng cao về Tổng hợp dao động
Các em có thể xem thêm phần hướng dẫn Giải bài tập Vật lý 12 Bài 5 để giúp các em nắm vững bài học và các phương pháp giải bài tập.
Bài tập 1 trang 25 SGK Vật lý 12
Bài tập 2 trang 25 SGK Vật lý 12
Bài tập 3 trang 25 SGK Vật lý 12
Bài tập 5 trang 25 SGK Vật lý 12
Bài tập 4 trang 25 SGK Vật lý 12
Bài tập 6 trang 25 SGK Vật lý 12
Bài tập 5.1 trang 13 SBT Vật lý 12
Bài tập 5.2 trang 13 SBT Vật lý 12
Bài tập 5.3 trang 14 SBT Vật lý 12
Bài tập 5.4 trang 14 SBT Vật lý 12
Bài tập 5.5 trang 14 SBT Vật lý 12
Bài tập 5.6 trang 14 SBT Vật lý 12
Bài tập 5.7 trang 14 SBT Vật lý 12
Bài tập 5.8 trang 15 SBT Vật lý 12
Bài tập 5.9 trang 15 SBT Vật lý 12
Bài tập 5.10 trang 15 SBT Vật lý 12
Bài tập 1 trang 60 SGK Vật lý 12 nâng cao
Bài tập 2 trang 60 SGK Vật lý 12 nâng cao
Bài tập 3 trang 60 SGK Vật lý 12 nâng cao
5. Hỏi đáp Bài 5 Chương 1 Vật lý 12
Trong quá trình học tập nếu có thắc mắc hay cần trợ giúp gì thì các em hãy comment ở mục Hỏi đáp, Cộng đồng Vật lý HOC247 sẽ hỗ trợ cho các em một cách nhanh chóng!
Chúc các em học tập tốt và luôn đạt thành tích cao trong học tập!
-- Mod Vật Lý 12 HỌC247