Phần hướng dẫn giải bài tập SGK Hình học 9 Bài 7 Vị trí tương đối của hai đường tròn sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng các dạng bài tập từ SGK Toán 9.
-
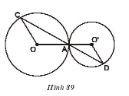
Bài tập 33 trang 119 SGK Toán 9 Tập 1
Trên hình 89 hai đường tròn tiếp xúc nhau tại A. Chứng minh rằng OC//O'D
-
Bài tập 34 trang 119 SGK Toán 9 Tập 1
Cho hai đường tròn (O; 20cm) và (O'; 15cm) cắt nhau tại A và B. Tính đoạn nối tâm OO', biết rằng AB=24cm. (Xét hai trường hợp: O và O' nằm khác phía đối với AB; O và O' nằm cùng phía đối với AB).
-
Bài tập 35 trang 122 SGK Toán 9 Tập 1
Điền vào các ô trống trong bảng, biết rằng hai đường tròn (O;R) và (O';r) có OO'=d, R>r
Vị trí tương đối của hai đường tròn
Số điểm chung
Hệ thức giữa \(d,\ R,\ r\)
\((O;\ R)\) đựng \((O;\ r)\)
\(d > R + r\)
Tiếp xúc ngoài
\(d = R - r\) \(2\)
-
Bài tập 36 trang 123 SGK Toán 9 Tập 1
Cho đường tròn tâm O bán kính OA và đường tròn đường kính OA
a) Hãy xác định vị trí tương đối của hai đường tròn
b) Dây AD của đường tròn lớn cắt đường tròn nhỏ ở C. Chứng minh rằng AC=CD
-
Bài tập 37 trang 123 SGK Toán 9 Tập 1
Cho hai đường tròn đồng tâm O. Dây AB của đường tròn lớn cắt đường tròn nhỏ ở C và D. Chứng minh rằng AC=BD.
-
Bài tập 38 trang 123 SGK Toán 9 Tập 1
Điền các từ thích hợp vào chỗ trống (...) :
a) Tâm của các đường tròn có bán kính 1cm tiếp xúc ngoài với đường tròn (O;3cm) nằm trên ...
b) Tâm của các đường tròn có bán kính 1cm tiếp xúc trong với đường tròn (O;3cm) nằm trên ...
-
Bài tập 39 trang 123 SGK Toán 9 Tập 1
Cho hai đường tròn (O) và (O') tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài BC, \(B\in (O),C\in (O')\). Tiếp tuyến chung trong tại A cắt tiếp tuyến chung ngoài BC ở I.
a) Chứng minh rằng
b) Tính số đo góc OIO'
c) Tính độ dài BC, biết \(OA=9cm, O'A=4cm\)
-
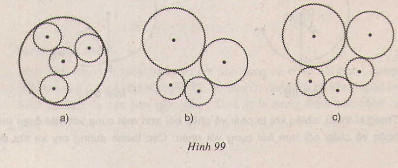
Bài tập 40 trang 123 SGK Toán 9 Tập 1
Trên các hình 99a, 99b, 99c, các bánh xe tròn có răng cưa được khớp với nhau. Trên hình nào hệ thống bánh răng chuyển động được? Trên hình nào hệ thống bánh răng không chuyển động được?
-
Bài tập 64 trang 167 SBT Toán 9 Tập 1
Cho hình \(76,\) trong đó hai đường tròn \((O)\) và \((O’)\) tiếp xúc nhau tại \(A.\) Chứng minh rằng các tiếp tuyến \(Bx\) và \(Cy\) song song với nhau.
-
Bài tập 65 trang 167 SBT Toán 9 Tập 1
Cho hai đường tròn \((O)\) và \((O’)\) cắt nhau tại \(A\) và \(B\) như trên hình \(77.\) Biết \(OA = 15cm,\) \(O’A = 13cm,\) \(AB = 24cm.\) Tính độ dài \(OO’.\)
-
Bài tập 66 trang 167 SBT Toán 9 Tập 1
Cho hai đường tròn \((O), (O’)\) tiếp xúc nhau tại \(A\) như trên hình \(78.\) Chứng minh rằng các bán kính \(OB\) và \(O’C\) song song với nhau.
-
Bài tập 67 trang 167 SBT Toán 9 Tập 1
Cho hai đường tròn \((O)\) và \((O’)\) cắt nhau tại \(A\) và \(B.\) Kẻ các đường kính \(AOC,\) \(AO’D.\) Chứng minh rằng ba điểm \(C, B, D\) thẳng hàng và \(AB ⊥ CD.\)
-
Bài tập 68 trang 168 SBT Toán 9 Tập 1
Cho hai đường tròn \((O)\) và \((O’)\) cắt nhau tại \(A\) và \(B.\) Gọi \(I\) là trung điểm của \(OO’.\) Qua \(A\) vẽ đường thẳng vuông góc với \(IA,\) cắt các đường tròn \((O)\) và \((O’)\) tại \(C\) và \(D\) (khác \(A\)). Chứng minh rằng \(AC = AD.\)
-
Bài tập 69 trang 168 SBT Toán 9 Tập 1
Cho hai đường tròn \((O)\) và \((O’)\) cắt nhau tại \(A\) và \(B,\) trong đó \(O’\) nằm trên đường tròn \((O).\) Kẻ đường kính \(O’OC\) của đường tròn \((O).\)
\(a)\) Chứng minh rằng \(CA, CB\) là các tiếp tuyến của đường tròn \((O’)\)
\(b)\) Đường vuông góc với \(AO’\) tại \(O’\) cắt \(CB\) ở \(I.\) Đường vuông góc với \(AC\) tại \(C\) cắt đường thẳng \(O’B\) ở \(K.\) Chứng minh rằng ba điểm \(O, I, K\) thẳng hàng.
-
Bài tập 70 trang 168 SBT Toán 9 Tập 1
Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Dây AC của đường tròn (O) tiếp xúc với đường tròn (O’) tại A. Dây AD của đường trong (O’) tiếp xúc với đường tròn (O) tại A. Gọi K là điểm đối xứng với A qua trung điểm I của OO’, E là điểm đối xứng với A qua B. Chứng minh rằng:
a. AB ⊥ KB
b. Bốn điểm A, C, E, D cùng nằm trên một đường tròn
-
Bài tập 7.1 trang 168 SBT Toán 9 Tập 1
Cho \(h.bs.23,\) trong đó \(OA = 3,\) \(O'A = 2,\) \(AB = 5.\) Độ dài \(AC\) bằng:

\((A)\) \(\displaystyle{{10} \over 3}\)
\((B)\) \(3,5\)
\((C)\) \(3\)
\((D)\) \(4.\)
Hãy chọn phương án đúng.
-
Bài tập 7.2 trang 168 SBT Toán 9 Tập 1
Cho hai đường tròn \((O)\) và \((O')\) cắt nhau tại \(A\) và \(B.\) Một đường thẳng vuông góc với \(AB\) tại \(B\) cắt các đường tròn \((O)\) và \((O')\) theo thứ tự tại \(C\) và \(D\) ( khác \(B\)). Chứng minh rằng \(OO’ =\displaystyle {1 \over 2}CD\).
-
Bài tập 71 trang 168 SBT Toán 9 Tập 1
Cho I là trung điểm của đoạn thẳng AB. Vẽ các đường tròn (I; IA) và (B; BA).
a. Hai đường tròn (I) và (B) nói trên có vị trí tương đối như thế nào với nhau? Vì sao?
b. Kẻ một đường thẳng đi qua A, cắt các đường tròn (I) và (B) theo thứ tự tại M và N. So sánh các độ dài AM và MN.
-
Bài tập 72 trang 169 SBT Toán 9 Tập 1
Cho hai đường tròn đồng tâm O. Gọi AB là dây bất kì của đường tròn nhỏ. Đường thẳng AB cắt đường tròn lớn ở C và D (A nằm giữa B và C). So sánh các độ dài AC và BD.
-
Bài tập 73 trang 169 SBT Toán 9 Tập 1
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Gọi CD là tiếp tuyến chung ngoài của hai đường tròn (C ∈ (O), D ∈ (O’))
a. Tính số đo góc CAD
b. Tính độ dài CD biết OA = 4,5cm, O’A = 2cm
-
Bài tập 74 trang 169 SBT Toán 9 Tập 1
Cho hai đường tròn đồng tâm O. Một đường tròn (O’) cắt một đường tròn tâm O tại A, B và cắt đường tròn tâm O còn lại tại C, D. Chứng minh rằng AB // CD.
-
Bài tập 75 trang 169 SBT Toán 9 Tập 1
Cho đường tròn \((O; 3cm)\) và đường tròn \((O’; 1cm)\) tiếp xúc ngoài tại \(A.\) Vẽ hai bán kính \(OB\) và \(O’C\) song song với nhau thuộc cùng nửa mặt phẳng có bờ \(OO’.\)
\(a)\) Tính số đo góc \(BAC.\)
\(b)\) Gọi \(I\) là giao điểm của \(BC\) và \(OO’.\) Tính độ dài \(OI.\)
-
Bài tập 76 trang 169 SBT Toán 9 Tập 1
Cho hai đường tròn \((O)\) và \((O’)\) tiếp xúc ngoài tại \(A.\) Kẻ các đường kính \(AOB, AO’C.\) Gọi \(DE\) là tiếp tuyến chung của hai đường tròn, \(D ∈ (O),\)\( E ∈ (O’).\) Gọi \(M\) là giao điểm của \(BD\) và \(CE.\)
\(a)\) Tính số đo góc \(DAE.\)
\(b)\) Tứ giác \(ADME\) là hình gì\(?\) Vì sao\(?\)
\(c)\) Chứng minh rằng \(MA\) là tiếp tuyến chung của hai đường tròn.
-
Bài tập 77 trang 169 SBT Toán 9 Tập 1
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài MN của hai đường tròn (M ∈ (O), N ∈ (O’)). Gọi P là điểm đối xứng với M qua OO’, Q là điểm đối xứng với N qua OO’. Chứng minh rằng:
a. MNQP là hình thang cân.
b. PQ là tiếp tuyến chung của hai đường tròn (O) và (O’).
c. MN + PQ = MP + NQ.
-
Bài tập 78 trang 170 SBT Toán 9 Tập 1
Cho hai đường tròn (O; 2cm), (O’; 3cm), OO’ = 6cm
a. Hai đường tròn (O) và (O’) có vị trí tương đối như thế nào với nhau?
b. Vẽ đường tròn (O’; 1cm) rồi kẻ tiếp tuyến OA với đường tròn đó (A là tiếp điểm). Tia O’A cắt đường tròn (O’; 3cm) ở B. Kẻ bán kính OC của đường tròn (O) song song với O’B, B và C thuộc cùng một nửa mặt phẳng có bờ OO’. Chứng minh rằng BC là tiếp tuyến chung của hai đường tròn (O; 2cm), (O’; 3cm).
c. Tính độ dài BC
d. Gọi I là giao điểm của BC và OO’/ Tính độ dài IO
-
Bài tập 79 trang 170 SBT Toán 9 Tập 1
Cho đường tròn (O; R), điểm A nằm bên ngoài đường tròn (R < OA < 3R). Vẽ đường tròn (A; 2R)
a. Hai đường tròn (O) và (A) có vị trí tương đối như thế nào với nhau?
b. Gọi B là một giao điểm của hai đường tròn trên. Vẽ đường kính BOC của đường tròn (O). Gọi D là giao điểm (khác C) của AC và đường tròn (O). Chứng minh rằng AD = DC
-
Bài tập 80 trang 170 SBT Toán 9 Tập 1
Cho đường tròn (O; 2cm) tiếp xúc với đường thẳng d. Dựng đường tròn (O’; 1cm) tiếp xúc với đường thẳng d và tiếp xúc ngoài với đường tròn (O).
-
Bài tập 8.1 trang 170 SBT Toán 9 Tập 1
Cho hai đường tròn (O;R) và (O’;r). Điền vào chỗ trống của bảng sau:
R r OO’ Hệ thức giữa OO’, R, r Vị trí tương đối của (O) và (O’) 3 1 ..... OO’ = R - r ..... 3 1 ..... ..... Tiếp xúc ngoài 3 1 3,5 ..... ..... 3 1 5 ..... ..... 3 1 1 ..... ..... -
Bài tập 8.2 trang 170 SBT Toán 9 Tập 1
Cho hai đường tròn (O; 3cm) và (O’; 4cm) có OO’ = 5cm.
a) Hai đường tròn (O) và (O’) có vị trí tương đối nào?
b) Tính độ dài dây chung của hai đường tròn.
-
Bài tập 8.3 trang 171 SBT Toán 9 Tập 1
Cho đường tròn (O) và điểm A cố định trên đường tròn. Điểm B chuyển động trên đường tròn.
a) Chứng minh rằng trung điểm M của AB chuyển động trên một đường tròn (O’).
b) Đường tròn (O’) có vị trí tương đối nào với đường tròn (O) ?