Bài tập 8.2 trang 170 SBT Toán 9 Tập 1

Hướng dẫn giải

Sử dụng kiến thức:

+) Nếu hai đường tròn \((O)\) và \((O')\)  cắt nhau nhau thì \(R-r<OO'<R+r.\)

+) Nếu hai đường tròn cắt nhau thì hai giao điểm đối xứng với nhau qua đường nối tâm, tức là đường nối tâm là đường trung trực của dây chung. 

Lời giải chi tiết

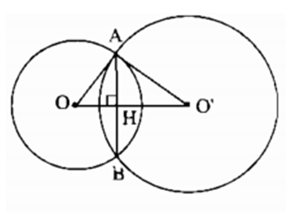
\(a)\) Ta có \(4-1<OO'=5<4+3\) \(\Rightarrow (O)\) và \((O’)\) cắt nhau.

\(b)\) Gọi \(A\) và \(B\) là giao điểm của hai đường tròn \((O)\) và \((O’),\) \(H\) là giao điểm của \(AB\) và \(OO’.\)

Ta có: \(5^2=3^2+4^2\) \((=25)\)

hay \(OO'^2=OA^2+O'A^2\)

\(\Rightarrow \Delta AOO'\) vuông tại \(A\) (định lý Pytago đảo)

Vì hai đường tròn \( (O)\) và \((O’)\) cắt nhau nên OO' là đường trung trực của AB.

Hay H là trung điểm của AB \(\Rightarrow AB = 2AH.\)

Xét \( \Delta AOO'\) vuông tại \(A\) có AH là chiều cao, theo hệ thức lượng trong tam giác vuông, ta có:

\(AH.OO'=OA.O'A\)

\(AH=\dfrac{OA.O'A}{OO'}=\dfrac{3.4}{5}\)

\(\Rightarrow AH=2,4 cm\)

Suy ra \(AB =2AH= 4,8cm.\)

-- Mod Toán 9 HỌC247