Bài tập 72 trang 169 SBT Toán 9 Tập 1

Hướng dẫn giải

Sử dụng kiến thức: Trong một đường tròn: 

+) Đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.

Lời giải chi tiết

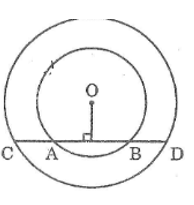
Kẻ \(OI ⊥ AB.\) Ta có: \(OI ⊥ CD\) 

Trong đường tròn \((O)\) (nhỏ) ta có: \(OI ⊥ AB\)

Suy ra: \(IA = IB\)   \((1)\) ( đường kính vuông góc dây cung thì đi qua trung điểm của dây ấy) 

Trong đường tròn \((O)\) (lớn) ta có: \(OI ⊥ CD\)

Suy ra: \(IC = ID\) ( đường kính vuông góc dây cung thì đi qua trung điểm của dây ấy)

Hay \(IA + AC = IB + BD    \)     \( (2)\)

Từ \((1)\) và \((2)\) suy ra: \(AC = BD.\)

-- Mod Toán 9 HỌC247