Bài tập 68 trang 168 SBT Toán 9 Tập 1

Hướng dẫn giải

Sử dụng kiến thức: 

+) Nếu các đường thẳng song song cách đều cắt một đường thẳng thì chúng chắn trên đường thẳng đó các đoạn thẳng liên tiếp bằng nhau.

+) Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.

Lời giải chi tiết

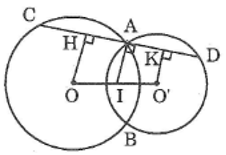
Kẻ \(OH ⊥ CD, O’K ⊥ CD\)

Ta có: \(IA ⊥ CD\)

Suy ra: \(OH // IA // O’K\)

Theo giả thiết: \(IO = IO’\)

Suy ra: \(AH = AK\)  \( (1)\) (tính chất đường thẳng song song cách đều)

Xét đường tròn (O) có \(OH ⊥ AC\) mà OH là 1 phần đường kính và AC là dây cung

Suy ra: \(HA = HC = \displaystyle {1 \over 2}AC\) (quan hệ giữa đường kính và dây cung)

\(⇒AC = 2AH   \;       (2)\)

Xét đường tròn (O') có \(O’K ⊥ AD\) mà O'K là 1 phần đường kính và AD là dây cung

Suy ra: \(KA = KD = \displaystyle {1 \over 2}AD\) ( quan hệ giữa đường kính và dây cung)

\(⇒ AD = 2AK     \;    (3)\)

Từ \((1), (2)\) và \((3)\) suy ra: \(AC = AD.\)

-- Mod Toán 9 HỌC247