Bài tập 74 trang 169 SBT Toán 9 Tập 1

Hướng dẫn giải

Sử dụng kiến thức:

+) Nếu hai đường tròn cắt nhau thì hai giao điểm đối xứng với nhau qua đường nối tâm, tức là đường nối tâm là trung trực của dây chung.

Lời giải chi tiết

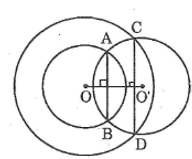
Vì đường tròn \((O’)\) cắt đường tròn \(( O; OA)\) tại \(A\) và \(B\) nên \(OO’\) là đường trung trực của \(AB\)

Suy ra: \(OO’ ⊥ AB\;\;         (1)\)

Vì đường tròn \((O’) \) cắt đường tròn \((O; OC)\) tại \(C\) và \(D\) nên \(OO’\) là đường trung trực của \(CD\)

Suy ra: \(OO’ ⊥ CD   \;\;       (2)\)

Từ \((1)\) và \((2)\) suy ra: \(AB // CD.\)

-- Mod Toán 9 HỌC247