Giải bài 76 tr 106 sách GK Toán 8 Tập 1
Chứng minh rằng các trung điểm của bốn cạnh của một hình thoi là các đỉnh của một hình chữ nhật.
Hướng dẫn giải chi tiết
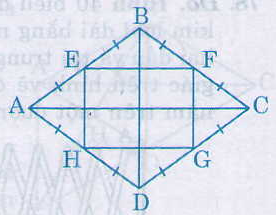
Xét hình thoi \(ABCD\), gọi \( E, F, G, H\) lần lượt là trung điểm của \( AB, BC, CD, AD\).
Ta có: \(EB = EA, FB = FC\) (giả thiết )
nên \(EF\) là đường trung bình của \(∆ABC\) (dấu hiệu nhận biết đường trung bình của tam giác )
\( \Rightarrow \) \(EF // AC,EF=\dfrac{AC}2\) (tính chất đường trung bình của tam giác)
Do \(HD = HA, GD = GC\) (giả thiết )
\( \Rightarrow \) \(HG\) là đường trung bình của \(∆ADC\) (dấu hiệu nhận biết đường trung bình của tam giác )
\( \Rightarrow \) \(HG // AC,HG=\dfrac{AC}2\) (tính chất đường trung bình của tam giác)
\( \Rightarrow \) \(EF // HG\) (cùng // \(AC\)) và \( EF=HG\,(=\dfrac{AC}2)\)
Suy ra \(EFGH\) là hình bình hành (dấu hiệu nhận biết hình bình hành)
Ta có: \(EB = EA, AH = HD\) (giả thiết )
nên \(EH\) là đường trung bình của \(∆ABD\) (dấu hiệu nhận biết đường trung bình của tam giác )
\( \Rightarrow \) \(EH // BD\) (tính chất đường trung bình của tam giác)
Ta có \(EF // AC\) (chứng minh trên) và \(BD ⊥ AC\) (tính chất hình thoi \(ABCD\))
\( \Rightarrow \) \(BD ⊥ EF\)
Mà \(EH // BD\) (chứng minh trên)
\( \Rightarrow \) \(EF ⊥ EH\)
\( \Rightarrow \) \(\widehat{FEH} = 90^0\)
Hình bình hành \(EFGH\) có \(\widehat{E} = 90^0\) nên là hình chữ nhật (dấu hiệu nhận biết hình chữ nhật)
-- Mod Toán 8 HỌC247
-


Hình thoi không có tính chất nào dưới đây?
bởi Hồng Hạnh
 16/01/2021
16/01/2021
A. Hai đường chéo cắt nhau tại trung điểm của mỗi đường
B. Hai đường chéo là các đường phân giác của các góc của hình thoi
C. Hai đường chéo bằng nhau
D. Hai đường chéo vuông góc với nhau
Theo dõi (0) 1 Trả lời -


A. bằng nhau
B. giao nhau tại trung điểm mỗi đường và vuông góc với nhau
C. giao nhau tại trung điểm mỗi đường
D. bằng nhau và giao nhau tại trung điểm mỗi đường
Theo dõi (0) 1 Trả lời -


Hãy chọn câu sai.
bởi lê Phương
 15/01/2021
15/01/2021
A. Tứ giác có 4 cạnh bằng nhau là hình thoi
B. Tứ giác có hai đường chéo vuông góc với nhau và bằng nhau là hình thoi
C. Hình bình hành có đường chéo là phân giác của một góc là hình thoi
D. Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi
Theo dõi (0) 1 Trả lời -


ho hình vuông ABCD. Lấy điểm M trên đường chéo AC. Vẽ ME vuông góc AD, MFvuông góc CD và MH vuông góc EF. Chứng minh rằng khi điểm M di động trên AC thì đường thẳng MH luôn đi qua một điểm cố định.
bởi Trần Hoàng Mai
 30/05/2020
Theo dõi (0) 1 Trả lời
30/05/2020
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC cân tại A, hai đường cao BE và CF cắt nhau tại H. Đường thẳng AH cắt EF tại D, cắt BC tại G. Gọi M và N lần lượt là hình chiếu của G trên AB và AC. Chứng minh rằng tứ giác DNGM là hình thoi.
bởi Nguyễn Thanh Trà
 30/05/2020
Theo dõi (1) 1 Trả lời
30/05/2020
Theo dõi (1) 1 Trả lời
Bài tập SGK khác
Bài tập 74 trang 106 SGK Toán 8 Tập 1
Bài tập 75 trang 106 SGK Toán 8 Tập 1
Bài tập 77 trang 106 SGK Toán 8 Tập 1
Bài tập 78 trang 106 SGK Toán 8 Tập 1
Bài tập 132 trang 96 SBT Toán 8 Tập 1
Bài tập 133 trang 96 SBT Toán 8 Tập 1
Bài tập 134 trang 97 SBT Toán 8 Tập 1
Bài tập 135 trang 97 SBT Toán 8 Tập 1
Bài tập 136 trang 97 SBT Toán 8 Tập 1
Bài tập 137 trang 97 SBT Toán 8 Tập 1
Bài tập 138 trang 97 SBT Toán 8 Tập 1
Bài tập 139 trang 97 SBT Toán 8 Tập 1
Bài tập 140 trang 97 SBT Toán 8 Tập 1
Bài tập 141 trang 97 SBT Toán 8 Tập 1
Bài tập 142 trang 97 SBT Toán 8 Tập 1
Bài tập 143 trang 97 SBT Toán 8 Tập 1
Bài tập 11.1 trang 97 SBT Toán 8 Tập 1





