Bài tập 137 trang 97 SBT Toán 8 Tập 1

Hướng dẫn giải

Vận dụng kiến thức: Tam giác cân có một góc bằng \(60^{\circ}\) là tam giác đều.

Lời giải chi tiết

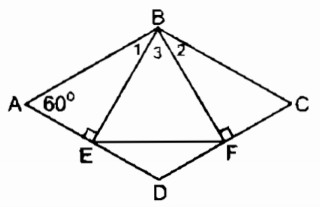
Xét hai tam giác vuông BEA và BFC:

\(\widehat {BEA} = \widehat {BFC} = {90^0}\)

\(\widehat A = \widehat C\) (tính chất hình thoi)

BA = BC (gt)

Do đó: ∆ BEA = ∆ BFC (cạnh huyền, góc nhọn)

⇒ BE = BF

⇒ ∆ BEF cân tại B

\( \Rightarrow {\widehat B_1} = {\widehat B_2}\)

⇒ Trong tam giác vuông BEA ta có:

\(\eqalign{  &  \Rightarrow \widehat A + {\widehat B_1} = {90^0} \Rightarrow {\widehat B_1} = {90^0} - \widehat A = {90^0} - {60^0} = {30^0}  \cr  &  \Rightarrow {\widehat B_2} = {\widehat B_1} = {30^0} \cr} \)

\( \Rightarrow \widehat A + \widehat {ABC} = {180^0}\) (hai góc trong cùng phía bù nhau)

\(\eqalign{  &  \Rightarrow \widehat {ABC} - {180^0} - \widehat A = {180^0} - {60^0} = {120^0}  \cr  &  \Rightarrow \widehat {ABC} = {\widehat B_1} + {\widehat B_2} + {\widehat B_3}  \cr  &  \Rightarrow {\widehat B_3} = \widehat {ABC} - \left( {{{\widehat B}_1} + {{\widehat B}_2}} \right)\cr  & = {120^0} - \left( {{{30}^0} + {{30}^0}} \right) = {60^0} \cr} \)

Vậy ∆ BEF đều.

-- Mod Toán 8 HỌC247